题目内容
试求出所有整数n,使得代数式2n2+n-29的值是某两个连续自然数的平方和.
解:设两个连续自然数是x、x+1,则根据题意知2n2+n-29=x2+(x+1)2,
化简为2x2+2x+30-2n2-n=0 ①
∴x=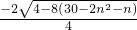 =
=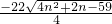 ②
②
因为x是自然数,所以4n2+2n-59必为某个整数的平方(完全平方数),
因此设4n2+2n-59=k2③
∴n=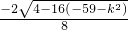 =
=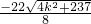 ④
④
因为n是整数,所以4k2+237必为某个整数的平方(完全平方数),
设4k2+237=a2⑤
则有a2-4k2=237,即(a+2k)(a-2k)=237,所以有
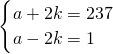 或
或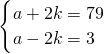 ,
,
解之得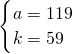 或
或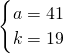
由⑤式得4k2+237=1192或412,
代入④式得n1=10,n2=-30,
∴符合条件的整数n是10或-30.
分析:先设两个连续自然数是x、x+1,然后根据题意列出方程,然后解以x为未知数的一元二次方程,然后利用多次方程有整数根的条件来解.
点评:本题主要考查了利用完全平方式的应用.两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.
化简为2x2+2x+30-2n2-n=0 ①
∴x=
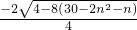 =
=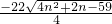 ②
②因为x是自然数,所以4n2+2n-59必为某个整数的平方(完全平方数),
因此设4n2+2n-59=k2③
∴n=
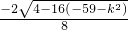 =
=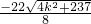 ④
④因为n是整数,所以4k2+237必为某个整数的平方(完全平方数),
设4k2+237=a2⑤
则有a2-4k2=237,即(a+2k)(a-2k)=237,所以有
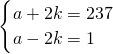 或
或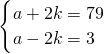 ,
,解之得
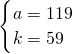 或
或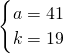
由⑤式得4k2+237=1192或412,
代入④式得n1=10,n2=-30,
∴符合条件的整数n是10或-30.
分析:先设两个连续自然数是x、x+1,然后根据题意列出方程,然后解以x为未知数的一元二次方程,然后利用多次方程有整数根的条件来解.
点评:本题主要考查了利用完全平方式的应用.两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.

练习册系列答案
相关题目









 图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为________.
图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为________. 如图所示,一只小鸟在地砖上自由觅食,它最终停在白色方砖上的概率为
如图所示,一只小鸟在地砖上自由觅食,它最终停在白色方砖上的概率为

 一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是
一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是

 与(+2)互为相反数
与(+2)互为相反数