题目内容
5.当x≠5时,分式$\frac{1}{x-5}$有意义;当x=-$\frac{1}{2}$时,分式$\frac{1-x}{2x+1}$无意义.分析 分式有意义,分母不等于0;分式无意义,分母等于0.
解答 解:当x-5≠0即x≠5时,分式$\frac{1}{x-5}$有意义;
当2x+1=0即x=-$\frac{1}{2}$时,分式$\frac{1-x}{2x+1}$无意义.
故答案是:x≠5;-$\frac{1}{2}$.
点评 本题考查了分式有意义的条件.从以下三个方面透彻理解分式的概念:
(1)分式无意义?分母为零;
(2)分式有意义?分母不为零;
(3)分式值为零?分子为零且分母不为零.

练习册系列答案
相关题目
20.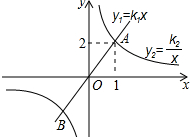 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,2),B(-1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,2),B(-1,-2)两点,若y1<y2,则x的取值范围是( )
 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,2),B(-1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,2),B(-1,-2)两点,若y1<y2,则x的取值范围是( )| A. | x<-1或x>1 | B. | x<-1或0<x<1 | C. | -1<x<0或0<x<1 | D. | -1<x<0或x>1 |
15.现定义一种新运算:a※b=b2-ab,如:1※2=22-1×2=2,则(-1※2)※3等于( )
| A. | -9 | B. | -6 | C. | 6 | D. | 9 |
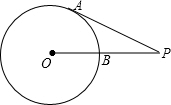 如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=12,BP=8,则⊙O的半径为5.
如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=12,BP=8,则⊙O的半径为5.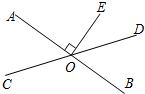 如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=52 度.
如图,直线AB.CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠AOC=52 度.
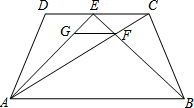 如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.
如图,在梯形ABCD中,AB∥CD,AD=BC,E是CD的中点,BE交AC于F,过点F作FG∥AB,交AE于点G.