题目内容
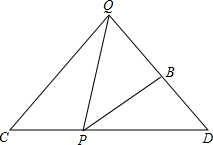 已知QC=QD=2,∠C=∠D=∠QPB=45°,P在CD上运动不与C、D重合,设CP=x,QB=y,求y关于x的函数关系式.
已知QC=QD=2,∠C=∠D=∠QPB=45°,P在CD上运动不与C、D重合,设CP=x,QB=y,求y关于x的函数关系式.考点:相似三角形的判定与性质
专题:常规题型
分析:易证△CPQ∽△DBP,可得
=
,可得BD关于x的函数式,即可解题.
| CQ |
| DP |
| CP |
| BD |
解答:解:∵∠C=∠D=∠QPB=45°.
∴∠CPQ+∠DPB=135°.
又∵∠CPQ+∠CQP=135°,
∴∠CQP=∠DPB.
∴△CPQ∽△DBP.
∴
=
;
∵CP=x,
∴PD=CD-CP=2
-x.
∴
=
,
∴2BD=2
x-x2.
∴BQ=DQ-BD=2-(
)=
x2-
x+2.
即y=
x2-
x+2.
∴∠CPQ+∠DPB=135°.
又∵∠CPQ+∠CQP=135°,
∴∠CQP=∠DPB.
∴△CPQ∽△DBP.
∴
| CQ |
| DP |
| CP |
| BD |
∵CP=x,
∴PD=CD-CP=2
| 2 |
∴
| 2 | ||
2
|
| x |
| BD |
∴2BD=2
| 2 |
∴BQ=DQ-BD=2-(
2
| ||
| 2 |
| 1 |
| 2 |
| 2 |
即y=
| 1 |
| 2 |
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=35°,则∠BAC的度数为( )| A、40° | B、45° |
| C、50° | D、55° |
若函数y=
,则当函数值y=8时,自变量x的值是( )
|
A、±
| ||
| B、4 | ||
C、±
| ||
D、-
|
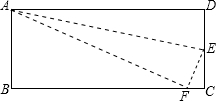 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,求DE的长.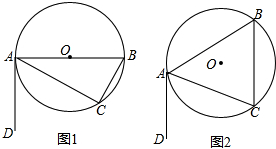 如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B.
如图1,⊙O中,AB为直径,AC为弦,过A作直线DA,使∠DAC=∠B. 如图,一个长方形放在桌面上,它的长宽高分别是3分米,3分米,8分米,一只蚂蚁想从底的点A沿盒的表面爬到盒顶B点处,请画图分析,并计算蚂蚁要爬行的最短路程是多少分米?
如图,一个长方形放在桌面上,它的长宽高分别是3分米,3分米,8分米,一只蚂蚁想从底的点A沿盒的表面爬到盒顶B点处,请画图分析,并计算蚂蚁要爬行的最短路程是多少分米? 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为