题目内容
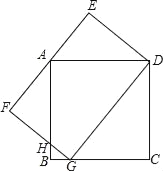
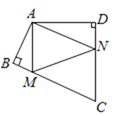
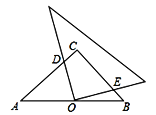
【题目】如图,在等腰直角![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 的中点,且AC=3,将一块直角三角板的直角顶点放在点
的中点,且AC=3,将一块直角三角板的直角顶点放在点![]() 处,始终保持该直角三角板的两直角边分别与
处,始终保持该直角三角板的两直角边分别与![]() 、
、![]() 相交,交点分别为
相交,交点分别为![]() 、
、![]() ,则
,则![]() ___________.
___________.
【答案】3
【解析】
连接CO,结合等腰直角三角形的性质可证明△ADO≌△COE,可证得AD=CE,则可求得CD+CE=AC=3.
如图,连接CO,

∵在等腰直角△ABC中,∠C=90°,点O是AB的中点,
∴CO=AO,∠A=∠OCB=45°,且∠AOC=90°,
∵∠DOE=90°,
∴∠AOD+∠DOC=∠DOC+∠COE=90°,
∴∠AOD=∠COE,
在△ADO和△COE中
∵∠A=∠OCE,AO=CO,∠AOD=∠COE
∴△ADO≌△COE(ASA),
∴AD=CE,
∴CD+CE=CD+AD=AC=3,
故答案为:3.

 应用题天天练四川大学出版社系列答案
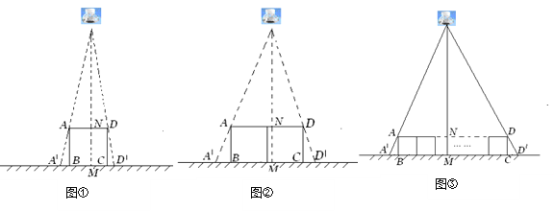
应用题天天练四川大学出版社系列答案【题目】如图,在某隧道建设工程中,需沿![]() 方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点
方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点![]() 在直线
在直线![]() 上,现在
上,现在![]() 上取一点
上取一点![]() ,
,![]() 外取一点
外取一点![]() ,测得
,测得![]() ,
,![]() ,
,![]() .求开挖点
.求开挖点![]() 到点
到点![]() 的距离.
的距离.
(精确到![]() 米)参考数据:
米)参考数据:![]() ,
,![]() ,
,![]() .
.

【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
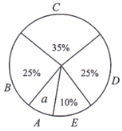
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.