Question

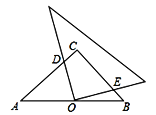
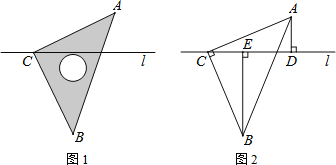
【题目】如图，已知BD，CE是△ABC的两条高，直线BD，CE相交于点H.

(1)若∠BAC＝100°，求∠DHE的度数；

(2)若△ABC中∠BAC＝50°，直接写出∠DHE的度数是____．

Answer 1

【答案】（1）∠DHE＝80°（2）50°或130°

【解析】

(1)根据已知条件可得∠HDA=∠AEH=90°，根据对顶角相等可得∠DAE的度数；

再根据四边形的内角和是360°便求出∠DHE的度数；

（2）需分两种情况讨论：当△ABC为锐角三角形时和当△ABC为钝角三角形时，分别求出∠DHE的度数即可.

（1）∵BD、CE是△ABC的两条高，

∴∠HDA=∠AEH=90°，

∵∠BAC=100°，

∴∠DAE=∠BAC=100°,

∴在四边形AEHD中，∠DHE=360°-∠HDA-∠DAE-∠AEH=80°，

（2）①当△ABC为锐角三角形时，∠DHE=180°-50°=130°，

②当△ABC为钝角三角形时，∠DHE=∠BAC=50°,

∴∠DHE的度数为130°或50°.