Question

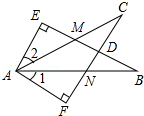如图∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：
①∠1=∠2；②CD=DN；③△ACN≌△ABM；④BE=CF．
其中正确的结论有

 

．

Answer 1

考点：全等三角形的判定与性质

专题：常规题型

分析：先利用“AAS”证明△ABE≌△ACF得到BE=CF；再根据三角形内角和定理由∠E=∠F=90°，∠B=∠C得到∠BAE=∠CAF，都减去∠CAB即可得到∠1=∠2；接着根据“AAS”证明△AEM≌△AFN得到AM=AN，则可证明△ACN≌△ABM；且得到AC=AB，AM=AN，则MC=BN，然后证明△DMC≌△DNB得到DC=DB，DM=DN，由于∠DNB＞∠C，则∠DNB＞∠B，所以DB＞DN，
于是得到CD＞DN．

解答：解：在△ABE和△ACF中，

∠E=∠F ∠B=∠C AE=AF

，
∴△ABE≌△ACF（AAS），
∴BE=CF，所以④正确；
∵∠E=∠F=90°，∠B=∠C，
∴∠BAE=∠CAF，
∴∠BAE-∠CAB=∠CAF-∠CAB，
即∠1=∠2，所以①正确；
在△AEM和△AFN中，

∠E=∠F ∠2=∠1 AE=AF

，
∴△AEM≌△AFN（AAS），
∴AM=AN，
在△ACN和△ABM中，

∠CAN=∠BAM ∠C=∠B AN=AM

，
∴△ACN≌△ABM（AAS），所以③正确；
∵AC=AB，AM=AN，
∴MC=BN，
在△DMC和△DNB中，

∠C=∠B ∠MDC=∠NDB MC=NB

，
∴△DMC≌△DNB（AAS），
∴DC=DB，DM=DN，
而∠DNB＞∠C，
∴∠DNB＞∠B，
∴DB＞DN，
∴CD＞DN，所以②错误．
故答案为①③④．

点评：本题考查∵了全等三角形的判定与性质：判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应角相等，对应边相等．