题目内容
 已知:如图,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从点A、C同时出发,均以2厘米/秒的速度分别沿AD向点D和沿CB向点B运动.设运动时间为t(其中t≤6.25)秒
已知:如图,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从点A、C同时出发,均以2厘米/秒的速度分别沿AD向点D和沿CB向点B运动.设运动时间为t(其中t≤6.25)秒(1)当EF与AC垂直时,求出t的值;
(2)在(1)的条件下,若P为线段AC上一点(点P不与点A、C重合),连结EP,当2AE2=AC•AP时,请判断EP与AD的位置关系,并说明理由;求出此时AP的长.
考点:四边形综合题
专题:
分析:(1)根据矩形的性质及勾股定理就可以求出AC的值,根据三角函数值就可以求出sin∠CAD和cos∠CAD的值,由条件可以得出△AOE≌△COF,就可以求出AO=CO,就可以求出AE的值而求出t的值;
(2)过E作EP⊥AD交AC于P,然后根据矩形的性质就可以证明△AOE∽△AEP,列出关系式就可以得出结论.
(2)过E作EP⊥AD交AC于P,然后根据矩形的性质就可以证明△AOE∽△AEP,列出关系式就可以得出结论.
解答:解:(1)∵EF⊥AC,
∴∠AOE=∠COF=90°.
∵四边形ABCD是矩形,
∴AB=CD,∠D=90°,AD∥BC,
∴∠CAD=∠ACB.
在△AOE和△COF中
,
∴△AOE≌△COF(AAS),
∴AO=CO,EO=FO.
在Rt△ADC中,由勾股定理,得
AC=20.
∴AO=
AC=10.
∵AB=12cm,AD=16cm,
∴CD=12.
∴cos∠CAD=
,
∴
=
,
∴
=
,
∴AE=
,
t=
÷2=
秒.
答:
时,EF与AC垂直;
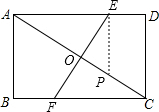
(2)过E作EP⊥AD交AC于P.
∴∠AEP=90°,
∴∠AEP=∠AOE.
∵∠OAE=∠EAP,
∴△AOE∽△AEP,
∴
=
,
∴AE2=A0•AP,
∴AE2=
AC•AP,
∴2AE2=AC•AP.
∴∠AOE=∠COF=90°.
∵四边形ABCD是矩形,
∴AB=CD,∠D=90°,AD∥BC,
∴∠CAD=∠ACB.
在△AOE和△COF中
|
∴△AOE≌△COF(AAS),
∴AO=CO,EO=FO.
在Rt△ADC中,由勾股定理,得
AC=20.
∴AO=
| 1 |
| 2 |
∵AB=12cm,AD=16cm,
∴CD=12.
∴cos∠CAD=
| 4 |
| 5 |
∴
| AO |
| AE |
| 4 |
| 5 |
∴
| 10 |
| AE |
| 4 |
| 5 |
∴AE=
| 25 |
| 2 |
t=
| 25 |
| 2 |
| 25 |
| 4 |
答:
| 25 |
| 4 |

(2)过E作EP⊥AD交AC于P.
∴∠AEP=90°,
∴∠AEP=∠AOE.
∵∠OAE=∠EAP,
∴△AOE∽△AEP,
∴
| AE |
| AP |
| AO |
| AE |
∴AE2=A0•AP,
∴AE2=
| 1 |
| 2 |
∴2AE2=AC•AP.
点评:本题考查了矩形的性质的运用,全等三角形的判定就性质的运用,勾股定理的运用,三角函数值的运用,相似三角形的判定及性质的运用,解答时证明三角形全等和相似是关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
4的算术平方根是( )
A、±
| ||
B、
| ||
| C、±2 | ||
| D、2 |
下列各式能用平方差公式计算的是( )
| A、(-3+x)(3-x) |
| B、(-a-b)(-b+a) |
| C、(-3x+2)(2-3x) |
| D、(3x+2)(2x-3) |
 如图,已知:AD∥BC,AD=CB,AE=CF,
如图,已知:AD∥BC,AD=CB,AE=CF,