题目内容
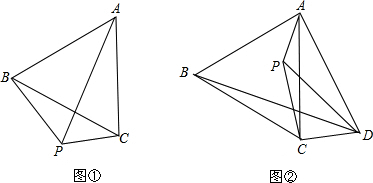
1. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,有下列四个条件:①AB=BE;②DE⊥DC;③∠ADB=90°;④CE⊥DE.如果添加其中一个条件就能使四边形DBCE成为矩形,那么这个条件是①或③或④.
分析 首先证明四边形DBCE是平行四边形,再添加所给条件,利用有一个角是直角的平行四边形是矩形进行判定即可.
解答 解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BC,
∵DE=AD,
∴DE=BC,
∴四边形DBCE是平行四边形,
添加①AB=BE,
∵AD=DE,
∴BD⊥AE,
∴∠EDB=90°,
∴四边形DBCE是矩形;
添加②不能使四边形DBCE成为矩形;
添加③∠ADB=90°,可得∠EDB=90°,可得四边形DBCE是矩形;
添加④CE⊥DE可得∠CED=90°,可得四边形DBCE是矩形;
故答案为:①或③或④.
点评 此题主要考查了矩形的判定,关键是掌握矩形的判定定理:有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目
11.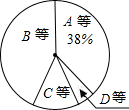 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
(1)在被调查的男生中,成绩为B等级的有23人,占被调查男生人数的46%,m=0.38;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).| 等级 | 成绩x/分 | 频数/(人数) | 频率 |
| A | 9.0≤x≤10.0 | a | m |
| B | 7.0≤x<9.0 | 23 | 0.46 |
| C | 6.0≤x<7.0 | b | n |
| D | 0.0≤x<6.0 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
16.已知:关于x的方程(m+1)x=n-1无解,则m,n的取值是( )
| A. | m=-1且n=1 | B. | m=-1且n≠1 | C. | m=n=0 | D. | m≠1且n=1 |
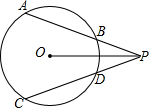 如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.
如图,已知过P点的两条直线交⊙O于A,B,C,D四点,且OP平分∠APC.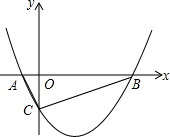 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.