题目内容
设x、y、z均为正实数,且满足
<
<
,则x、y、z三个数的大小关系是 .
| z+2x+2y |
| x+y |
| x+2y+2z |
| y+z |
| y+2x+2z |
| z+x |
考点:不等式的性质
专题:
分析:由
<
<
可知,
+2<
+2<
+2,从而可知,
<
<
,
>
>
,
+1>
+1>
+1,从而得到结论.
| z+2x+2y |
| x+y |
| x+2y+2z |
| y+z |
| y+2x+2z |
| z+x |
| z |
| x+y |
| x |
| y+z |
| y |
| z+x |
| z |
| x+y |
| x |
| y+z |
| y |
| z+x |
| x+y |
| z |
| y+z |
| x |
| z+x |
| y |
| x+y |
| z |
| y+z |
| x |
| z+x |
| y |
解答:解:∵
<
<
,
∴
+2<
+2<
+2
∴
<
<
,
>
>
,
+1>
+1>
+1,
即
>
>
.
∴z<x<y
故答案为:z<x<y.
| z+2x+2y |
| x+y |
| x+2y+2z |
| y+z |
| y+2x+2z |
| z+x |
∴
| z |
| x+y |
| x |
| y+z |
| y |
| z+x |
∴
| z |
| x+y |
| x |
| y+z |
| y |
| z+x |
| x+y |
| z |
| y+z |
| x |
| z+x |
| y |
| x+y |
| z |
| y+z |
| x |
| z+x |
| y |
即
| x+y+z |
| z |
| y+z+x |
| x |
| z+x+y |
| y |
∴z<x<y
故答案为:z<x<y.
点评:本题考查了不等式的性质,解题的关键是利用不等式的性质在不等式的两边同加上常数进行变形,有一定难度.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
某区2009年应届初中毕业生为5.5万人,2010年、2011年两届毕业生一共为12.5万人,设2009年到2011年平均每年学生人数增长的百分率为x,则方程可列为( )
| A、5.5(1+x)2=12.5 |
| B、5.5+5.5(1+x)2=12.5 |
| C、5.5+5.5(1+x)+5.5(1+x)2=12.5 |
| D、5.5(1+x)+5.5(1+x)2=12.5 |
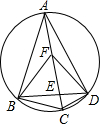 如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:
如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:①线段AC为⊙O的直径;②CD⊥DF;③BC=2CD;④∠AFB=∠BCD
其中正确的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
函数y=
的自变量x的取值范围是( )
| -1-2x |
A、x≥-
| ||
B、x≤-
| ||
C、x≥
| ||
D、x≤
|
 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m 的解集为
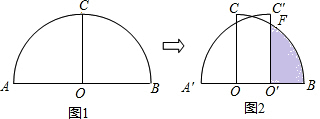
 如图,请证明在同一三角形中,等边对等角.
如图,请证明在同一三角形中,等边对等角. 如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C.在图中画出△A′B′C,并分别写出点A′、B′、C的坐标.
如图,若将△ABC绕点C逆时针旋转90°后得到△A′B′C.在图中画出△A′B′C,并分别写出点A′、B′、C的坐标.