题目内容
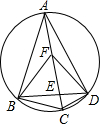 如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:
如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:①线段AC为⊙O的直径;②CD⊥DF;③BC=2CD;④∠AFB=∠BCD
其中正确的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:圆周角定理,等腰三角形的判定与性质
专题:
分析:根据圆周角定理、等腰三角形的判定与性质等,作出辅助线,根据有关性质和定理对每一结论进行证明即可得出答案.
解答:解:①∵AB=AD,
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°-∠BAD)÷2=90°-∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF,
∴∠FDC=90°,
∴∠ADC>90°,
∴线段AC不为⊙O的直径,
∴①错误,②正确;
③过F作FG⊥BC,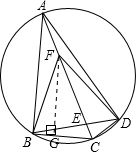
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ACB=∠ADB,
∠BFC=∠BAD,
∴∠FBC=∠ABD,
∴∠FBC=∠ADB,
∴∠FBC=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,∠GFC=
∠BAD=∠DFC.
∴△FGC≌△DFC(∠GFC=∠DFC,FC=FC,∠ACB=∠ACD).
∴CD=GC=
BC.
∴BC=2CD,
∴③正确;
④∵∠BFC=∠BAD,
∠AFB=180°-∠BFC,
∠BCD=180°-∠BAD,
∴∠AFB=∠BCD
∴④正确;
其中正确的个数为3个.
故选D.
∴弧AB=弧AD,∠ADB=∠ABD.
∵∠ACB=∠ADB,∠ACD=∠ABD,
∴∠ACB=∠ADB=∠ABD=∠ACD.
∴∠ADB=(180°-∠BAD)÷2=90°-∠DFC.
∴∠ADB+∠DFC=90°,即∠ACD+∠DFC=90°,
∴CD⊥DF,
∴∠FDC=90°,
∴∠ADC>90°,
∴线段AC不为⊙O的直径,
∴①错误,②正确;
③过F作FG⊥BC,

∵AB=AD,
∴∠ABD=∠ADB,
∵∠ACB=∠ADB,
∠BFC=∠BAD,
∴∠FBC=∠ABD,
∴∠FBC=∠ADB,
∴∠FBC=∠ACB.
∴FB=FC.
∴FG平分BC,G为BC中点,∠GFC=
| 1 |
| 2 |
∴△FGC≌△DFC(∠GFC=∠DFC,FC=FC,∠ACB=∠ACD).
∴CD=GC=
| 1 |
| 2 |
∴BC=2CD,
∴③正确;
④∵∠BFC=∠BAD,
∠AFB=180°-∠BFC,
∠BCD=180°-∠BAD,
∴∠AFB=∠BCD
∴④正确;
其中正确的个数为3个.
故选D.
点评:本题考查了圆周角定理;用到的知识点为圆周角定理、等腰三角形的判定与性质等,解题的关键是作出辅助线根据有关性质和定理对每一结论进行证明.

练习册系列答案
相关题目
某段公路由上坡、平坡、下坡三个等长的路段组成,已知一辆汽车在三个路段上行驶的平均速度分别为v1,v2,v3,则此辆汽车在这段公路上行驶的平均速度为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若(a
=
,如5
=
),x>1,y>0,且满足xy=xy,
=x3y,则x+y的值为( )
| 1 |
| n |
| n | a |
| 1 |
| 3 |
| 3 | 5 |
| x |
| y |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
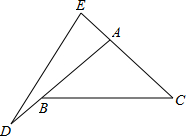 如图所示,在△ABC中,AB=AC,延长AB到D,延长CA到E,使AD=CE=BC.若恰好有DE=BC,求∠BAC的大小.
如图所示,在△ABC中,AB=AC,延长AB到D,延长CA到E,使AD=CE=BC.若恰好有DE=BC,求∠BAC的大小. 如图,一个六边形的六个内角都是120°,连续四边的长依次是2.7,3,5,2,求该六边形周长.
如图,一个六边形的六个内角都是120°,连续四边的长依次是2.7,3,5,2,求该六边形周长.