题目内容
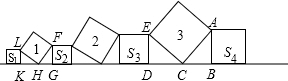
在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+S2+S3+S4等于（ ）| A、4 | B、5 | C、6 | D、14 |
考点：全等三角形的判定与性质,勾股定理,正方形的性质
专题：
分析：如图，易证△CDE≌△ABC，得AB2+DE2=DE2+CD2=CE2，同理FG2+LK2=HL2，S1+S2+S3+S4=1+3=4．
解答：解：∵在△CDE和△ABC中，
，
∴△CDE≌△ABC（AAS），
∴AB=CD，BC=DE，
∴AB2+DE2=DE2+CD2=CE2=3，
同理可证FG2+LK2=HL2=1，
∴S1+S2+S3+S4=CE2+HL2=1+3=4．
故选A．
|
∴△CDE≌△ABC（AAS），
∴AB=CD，BC=DE，
∴AB2+DE2=DE2+CD2=CE2=3，
同理可证FG2+LK2=HL2=1，
∴S1+S2+S3+S4=CE2+HL2=1+3=4．
故选A．
点评：本题考查了全等三角形的证明，考查了勾股定理的灵活运用，本题中证明AB2+DE2=DE2+CD2=CE2是解题的关键．
练习册系列答案
相关题目
如果|a|=|b|，那么（ ）
| A、a=b |
| B、a+b=0 |
| C、a=b或a+b=0 |
| D、a=b=0 |
已知等腰三角形一腰上的中线把周长分为15和27两部分，则这个等腰三角形的底边长是（ ）
| A、6 | B、22 |
| C、6或22 | D、10或18 |
-（-
）的相反数是（ ）
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
在-
，
，0，3.14，-
，0.
2
，-
，-3
中，无理数的个数有（ ）
| 1 |
| 7 |
| π |
| 2 |
| 2 |
| • |
| 3 |
| • |
| 6 |
| 49 |
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知：如图，AB是⊙O的直径，点D在⊙O上，OC∥AD交⊙O于E，点F在CD延长线上，且∠BOC+∠ADF=90°．求证：CD是⊙O的切线．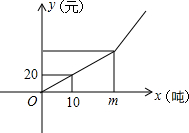
某市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费