题目内容
如图，AB切⊙O于点B，AB=4cm，AO=6cm，则⊙O的半径为________cm．
分析：连接OB，根据切线的性质知道∠B=90°，然后由勾股定理得OB2=AO2-AB2即可求出OB．
解答：
解：如图，连接OB，∵AB切⊙O于点B，
∴∠B=90°，
∴在Rt△ABO中，OB2=AO2-AB2，
∴OB=2
．故填空答案：2
．点评：本题利用了切线的性质，勾股定理求解，比较简单．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
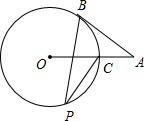已知：如图，AB切⊙O于点B，OA与⊙O交于点C，点P在⊙O上，若∠BAC=40°，则∠BPC的度数为（ ）| A、20° | B、25° | C、30° | D、40° |
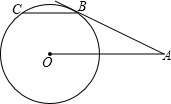如图，AB切⊙O于点B，OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
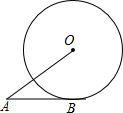如图，AB切⊙O于点B，AB=4cm，AO=6cm，则⊙O的半径为
（2012•西藏）如图，AB切⊙O于点B，延长AO交⊙O于点C，连接BC．若∠A=40°，则∠C=（ ）
（2012•广东模拟）如图，AB切⊙O于点A，OD⊥弦AC于点D，延长OD，交AB于点B，若∠O=60°，AC=6cm，则AB=