题目内容
13．在△ABC中，AB=AC=6，cos∠B=$\frac{2}{3}$，以点B为圆心，AB为半径作圆B，以点C为圆心，半径长为13作圆C，圆B与圆C的位置关系是（ ）| A． | 外切 | B． | 相交 | C． | 内切 | D． | 内含 |
分析 解直角三角形得到BC=8，得到6+13＞8，于是得到结论．
解答 解：∵AB=AC=6，cos∠B=$\frac{2}{3}$，
∴BC=8，
∵以点B为圆心，AB为半径作圆B，以点C为圆心，半径长为13作圆C，
∴6+13＞8，
∴圆B与圆C的位置关系是相交，
故选B．
点评 本题考查了圆与圆的位置关系，熟悉5种位置关系，是解答此题的关键．
练习册系列答案
相关题目
3．
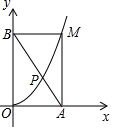如图，点M是抛物线y=ax2（x＞0）上的任意一点，MA⊥x轴于点A，MB⊥y轴于点B，连接AB，交抛物线于点P，则$\frac{PA}{PB}$的值是（ ）
如图，点M是抛物线y=ax2（x＞0）上的任意一点，MA⊥x轴于点A，MB⊥y轴于点B，连接AB，交抛物线于点P，则$\frac{PA}{PB}$的值是（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{3-\sqrt{5}}{2}$ | D． | $\frac{3+\sqrt{5}}{2}$ |
4．
如图，在矩形ABCD中，AD=$\sqrt{2}$AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；
②OE=OD；
③BH=HF；
④BC-CF=2HE；
⑤AB=HF．
其中正确的有（ ）
如图，在矩形ABCD中，AD=$\sqrt{2}$AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；
②OE=OD；
③BH=HF；
④BC-CF=2HE；
⑤AB=HF．
其中正确的有（ ）
| A． | ①②③④⑤ | B． | ①②③④ | C． | ①③④⑤ | D． | ①②③⑤ |
如图，矩形ABCD中，AD=10，AB=8，点E为边DC上一动点，连接AE，把△ADE沿AE折叠，使点D落在点D′处，当△DD′C是直角三角形时，DE的长为4或5．
18．
如图，直线a，b被直线c所截，若a∥b，∠1=40°，∠2=70°，则∠3=（ ）
如图，直线a，b被直线c所截，若a∥b，∠1=40°，∠2=70°，则∠3=（ ）| A． | 70° | B． | 100° | C． | 110° | D． | 120° |
如图，一次函数y=-$\frac{2}{3}$x+$\frac{4}{3}$的图象与反比例函数y=$\frac{k}{x}$（x＜0）的图象交于点A，与x轴交于点B，△AOB的面积为2，则k的值等于-2．
2．
如图，直线b、c被直线a所截，则∠1与∠2是（ ）
如图，直线b、c被直线a所截，则∠1与∠2是（ ）| A． | 同位角 | B． | 同旁内角 | C． | 内错角 | D． | 对顶角 |
3．顺次连结四边形四条边的中点，所得的四边形是矩形，则原四边形一定是（ ）
| A． | 平行四边形 | B． | 对角线相等的四边形 | ||
| C． | 对角线互相垂直的四边形 | D． | 矩形 |