题目内容
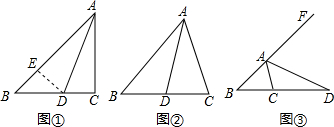
19.如图,在△ABC中,∠ACB=2∠B.(1)如图①,当∠C=90°,AD为∠BAC的平分线时,求证:AB=AC+CD;
(2)如图②,当∠C≠90°,AD为∠BAC的平分线时,线段AB,AC,CD有怎样的数量关系?不需要证明,直接写出你的猜想;
(3)如图③,当AD为∠BAC的外角平分线时,线段AB,AC,CD有怎样的数量关系?写出你的猜想,并对你的猜想给予证明.
分析 (1)AB=AC+CD.首先在AB上截取AE=AC,连接DE,易证△ADE≌△ADC(SAS),则可得∠AED=∠C,ED=CD,又由∠AED=∠ACB,∠ACB=2∠B,所以∠AED=2∠B,即∠B=∠BDE,易证DE=CD,则可求得AB=AC+CD;
(2)AC+AB=CD.首先在BA的延长线上截取AE=AC,连接ED,易证△EAD≌△CAD,可得ED=CD,∠AED=∠ACD,又由∠ACB=2∠B,易证DE=EB,则可求得AC+AB=CD.
(3)AB=CD-AC,理由为:在AF上截取AG=AC,如图3所示,同(2)即可得证.
解答 解:(1)过D作DE⊥AB,交AB于点E,如图①,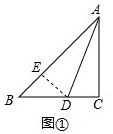
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,$\left\{\begin{array}{l}{DE=DC}\\{AD=AD}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由:
在AB上截取AG=AC,如图②,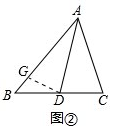
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
在△ADG和△ADC中,$\left\{\begin{array}{l}{AG=AC}\\{∠GAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADG≌△ADC(SAS),
∴CD=CG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CD-AC,理由:
在AF上截取AG=AC,如图③,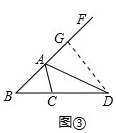
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
在△ADG和△ACD中,$\left\{\begin{array}{l}{AG=AC}\\{∠GAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BG-AG=CD-AC.
点评 此题是三角形综合题,主要考查了全等三角形的判定与性质,角平分线的性质,等腰直角三角形的判定和性质的综合应用,正确作出辅助线构造全等三角形并运用全等三角形的对应边相等是解题的关键.

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
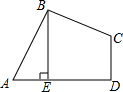 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于2.
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于2.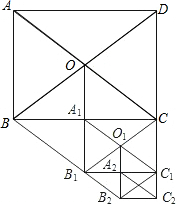 如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$.
如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$.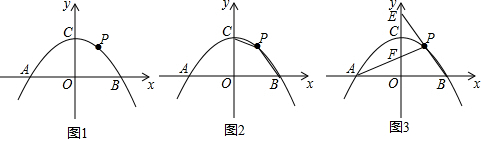
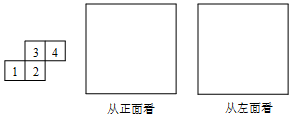 一个几何体是由几个大小相同的小立方块搭成的,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数请画出从正面、左面看到的这个几何体的形状图.
一个几何体是由几个大小相同的小立方块搭成的,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数请画出从正面、左面看到的这个几何体的形状图.