题目内容
15．某中学七年级A班有50人，某次活动中分为四组，第一组有a人，第二组比第一组的一半多6人，第三组的人数等于前两组人数的和．（1）求第三组的人数．（用含a的式子表示）
（2）求第四组的人数．（用含a的式子表示）
（3）试判断a=2时，是否满足题意．
分析 （1）根据第一组有a人，第二组比第一组的一半多6人，第三组的人数等于前两组人数的和分别表示出前3组；
（2）用总人数减去前3组即可表示出第4组；
（3）直接把a=2代入（1）中计算即可判断．
解答 解：（1）第一组：a人； 第二组：$\frac{1}{2}$a+6；第三组：a+$\frac{1}{2}$a+6=$\frac{3}{2}$a+6；
（2）第四组：50-a-（$\frac{1}{2}$a+6）-（ $\frac{3}{2}$a+6）=50-a-$\frac{1}{2}$a-6-$\frac{3}{2}$a-6=38-3a；
（3）当a=2时，第4组的人数为38-6=32（人），符合题意．
点评 此题考查了整式的加减，以及列代数式，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
已知抛物线y=ax2+bx+c与x轴交于A（-1，0）和B（2，0），与y轴交于点C（0，-2）．
如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，求菱形ABCD的周长．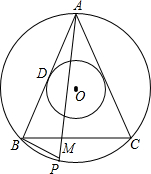
如图，已知△ABC内接于以点O为同心圆的大圆⊙O，且AB=AC，腰AB切小圆⊙O于点D．P是$\widehat{BC}$上的动点（不与点B、C重合），AP交BC于点M．
如图，P为菱形ABCD的对角线AC上一点，若PB=3，则PD=3．（填“＞”或“=”或“＜”号）
4．若关于x的方程$\frac{|x|}{x+4}$=kx2有四个不同的实数解，则k的取值范围为（ ）
| A． | （0，1） | B． | （$\frac{1}{4}$，1） | C． | （$\frac{1}{4}$，+∞） | D． | （1，+∞） |
材料：一般地，对于任意的a、b，由多项式的乘法法则可以得到