题目内容
8.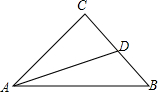 已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC.
已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC.
分析 在AB上截取AE=AC,连接DE,于是得到BE=CD,根据角平分线的定义得到∠CAD=∠EAD,推出△ACD≌△ADE,根据全等三角形的性质得到DE=CD,∠C=∠AED,于是得到DE=BE,根据等腰三角形的性质得到∠B=∠BDE,∠CAB=∠B,等量代换得到∠C=∠DEB=∠DEA,即可得到结论.
解答 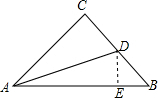 证明:在AB上截取AE=AC,连接DE,
证明:在AB上截取AE=AC,连接DE,
∵AB=AC+CD,
∴BE=CD,
∵AD平分∠CAB,
∴∠CAD=∠EAD,
在△ACD与△ADE中,$\left\{\begin{array}{l}{AC=AE}\\{∠CAD=∠EAD}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△ADE,
∴DE=CD,∠C=∠AED,
∴DE=BE,
∴∠B=∠BDE,
∵AC=BC,
∴∠CAB=∠B,
∴∠C=∠DEB=∠DEA,
∴∠DEA=$\frac{1}{2}×$180°=90°,
∴∠C=90°,
∴AC⊥BC.
点评 此题考查全等三角形的判定和性质,等腰三角形的判定和性质,正确作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
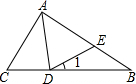 如图所示,在△ABC中,∠C=2∠B,AD是∠CAB的平分线,∠B=∠1,ED=EB.
如图所示,在△ABC中,∠C=2∠B,AD是∠CAB的平分线,∠B=∠1,ED=EB.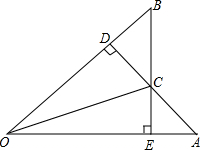 如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.
如图,AE=BD,AD⊥OB于点D,BE⊥OA于点E,AD、BE交于点C.连OC,求证:OC平分∠AOB.