题目内容
17.如图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,…,依此类推,则a12的值是156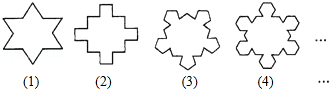
分析 观察可得边数与扩展的正n边形的关系为n×(n+1),把n=5代入求解即可.
解答 解:∵n=3时,边数为3×4=12;
n=4时,边数为4×5=20;
n=5时,边数为5×6=30;
…
∴a12=12×13=156.
故答案为:156.
点评 本题考查了图形的变化规律性,得到边数与扩展的正n边形的关系是解决本题的关键.

练习册系列答案
相关题目
8.已知点P(-2,1),那么点P关于y轴对称的点Q的坐标是( )
| A. | (-2,1) | B. | (-2,-1) | C. | (-1,2) | D. | (2,1) |
6.下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2-3xy+4=0,③x2-$\frac{1}{x}$=4,④x2=0.
①3x2+x=20,②2x2-3xy+4=0,③x2-$\frac{1}{x}$=4,④x2=0.
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ①④ |
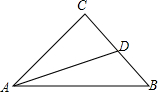 已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC.
已知:CA=CB,AD平分∠CAB,且AB=AC+CD,求证:AC⊥BC. 由图填空:
由图填空: