题目内容
x取何值时,下列各式有意义?
(1)
:
(2)
:
(3)
:
(1)
| 4-x |
x≤4
x≤4
; (2)
| 3 | 4+x |
x为任何数
x为任何数
;(3)
| ||
| x-2 |
x≥-
且x≠2
| 1 |
| 2 |
x≥-
且x≠2
.| 1 |
| 2 |
分析:(2)根据二次根式的意义得出4-x≥0,求出即可;
(2)根据立方根的意义得出4+x为任何数都可以,求出即可;
(3)根据二次根式的意义和分式的定义得出2x+1≥0且x-2≠0,求出即可.
(2)根据立方根的意义得出4+x为任何数都可以,求出即可;
(3)根据二次根式的意义和分式的定义得出2x+1≥0且x-2≠0,求出即可.
解答:解:(1)∵要使
有意义,必须4-x≥0,
∴x≤4;
(2)∵要使
有意义,必须4+x为任何数都可以,
∴x为任何数;
(3)要使
有意义,必须2x+1≥0且x-2≠0,
∴x≥-
且x≠2.
故答案为:x≤4;x为任何数;x≥-
且x≠2.
| 4-x |
∴x≤4;
(2)∵要使
| 3 | 4+x |
∴x为任何数;
(3)要使
| ||
| x-2 |
∴x≥-
| 1 |
| 2 |
故答案为:x≤4;x为任何数;x≥-
| 1 |
| 2 |
点评:本题考查了二次根式的意义,立方根的定义,分式的定义的应用,主要考查学生的理解能力和计算能力.

练习册系列答案
相关题目
 :______;
:______;  :______;
:______; :______.
:______. ;
; ;
; ;
; ;
;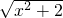 .
. ;
; ;
; ;
; .
.