题目内容
在△ABC中,AB=AC,∠A=36°,∠B的平分线交AC于D,AC=2,则AD= .
考点:黄金分割
专题:
分析:根据等腰三角形的性质和三角形内角和定理得到∠ABC=∠C=72°,再利用角平分线的定义得∠ABD=
∠ABC=36°,则DA=DB,于是可证明△BDC∽△ABC,利用相似比得到CD:BC=BC:AC,利用等线段代换得到CD:AD=AD:AC,于是可根据黄金分割的定义得到AD=
AC.
| 1 |
| 2 |
| ||
| 2 |
解答: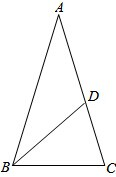 解:如图,∵AB=AC,∠A=36°,
解:如图,∵AB=AC,∠A=36°,
∴∠ABC=∠C=
(180°-36°)=72°,
∵∠ABC的平分线BD与AC交于D,
∴∠ABD=
∠ABC=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∵∠C=∠ABC=∠BDC=72°,
∴△BDC∽△ABC,
∴CD:BC=BC:AC,
∴CD:AD=AD:AC,
∴AD=
AC=
-1.
故答案为:
-1.
 解:如图,∵AB=AC,∠A=36°,
解:如图,∵AB=AC,∠A=36°,∴∠ABC=∠C=
| 1 |
| 2 |
∵∠ABC的平分线BD与AC交于D,
∴∠ABD=
| 1 |
| 2 |
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∵∠C=∠ABC=∠BDC=72°,
∴△BDC∽△ABC,
∴CD:BC=BC:AC,
∴CD:AD=AD:AC,
∴AD=
| ||
| 2 |
| 5 |
故答案为:
| 5 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
相关题目
以下说法正确的是( )
| A、非负数的绝对值等于本身的数 |
| B、非正数的相反数等于本身的数 |
| C、倒数等于本身的数有±1,0 |
| D、两个负数,绝对值大的仍然大 |
若x的相反数是3,|y|=5,则x+y的值为( )
| A、8或-2 | B、2 |
| C、-8或2 | D、-8 |
n个连续自然数按规律排列如下:

根据规律,2005所在位置为( )

根据规律,2005所在位置为( )
| A、第1002列,第1行 |
| B、第1002列,第2行 |
| C、第1003列,第1行 |
| D、第1003列,第2行 |