题目内容
4.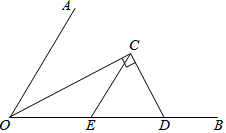 如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.
如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.(1)判断△CED的形状,并说明理由;
(2)若OC=3,求CD的长.
分析 (1)△CED为等边三角形,理由如下:由OC为角平分线及∠AOB度数求出∠AOC与∠COE度数,再由CE与OA平行,得到一对内错角相等,再由CD与OC垂直,求出∠ECD度数,利用三个内角相等的三角形为等边三角形即可得证;
(2)由△CED为等边三角形,得到三边相等,利用等角对等边得到OE=CE,进而得到OE=CE=DE,设CD=x,利用30度角所对的直角边等于斜边的一半得到OD=2x,再由OC的长,利用勾股定理列出方程,求出方程的解得到x的值,即可确定出CD的长.
解答 解:(1)△CED是等边三角形,理由如下:
∵OC平分∠AOB,∠AOB=60°,
∴∠AOC=∠COE=30°,
∵CE∥OA,
∴∠AOC=∠COE=∠OCE=30°,∠CED=60°,
∵CD⊥OC,
∴∠OCD=90°,
∴∠EDC=60°,
∴△CED是等边三角形;
(2)∵△CED是等边三角形,
∴CD=CE=ED,
又∵∠COE=∠OCE,
∴OE=EC,
∴CD=ED=OE,
设CD=x,则OD=2x,
在Rt△OCD中,根据勾股定理得:x2+9=4x2,
解得:x=$\sqrt{3}$,
则CD=$\sqrt{3}$.
点评 此题考查了等边三角形的判定与性质,勾股定理,平行线的性质,含30度直角三角形的性质,熟练掌握等边三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.
如图,△ABC中,AB=AC=10,BC=12,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的面积是12.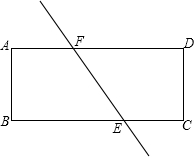 如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.
如图,直线EF将矩形纸片ABCD分成面积相等的两部分,E、F分别与BC交于点E,与AD交于点F(E,F不与顶点重合).设AB=a,AD=b,BE=x.用剪刀将纸片沿直线EF剪开后,将纸片ABEF沿AB翻折,再平移拼接在梯形ECDF的下方,那么能否做到纸片ABEF的一边与EC重合,另一边落在DC的延长线上,能(用“能”或“不能”填空).若填“能”,我们把拼接后在下方的四边形记作ECB′E′,当$\frac{x}{b}$的值为$\frac{2}{3}$或$\frac{1}{3}$时,直线E′E经过原矩形的一个顶点,若填“不能”,请说明理由:不能.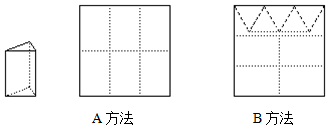
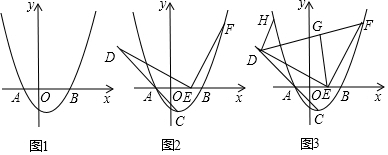
 如图,已知线段a,h(a>h),求作等腰三角形ABC,使AB=AC=a,底边BC上的高AD=h(保留作图痕迹,不要求写出作法).
如图,已知线段a,h(a>h),求作等腰三角形ABC,使AB=AC=a,底边BC上的高AD=h(保留作图痕迹,不要求写出作法).