题目内容
(1)计算:-12014+(4-π)0-cos45°+(
)-1-
;
(2)先化简,再求值:
÷(
-m-2),其中m=
-3.
| 2 |
| 1 | ||
1-
|
(2)先化简,再求值:
| m-3 |
| 2m-4 |
| 5 |
| m-2 |
| 2 |
考点:二次根式的混合运算,分式的化简求值,零指数幂,负整数指数幂,特殊角的三角函数值
专题:计算题
分析:(1)原式第一项利用乘方的意义化简,第二项利用零指数幂法则计算,第三项利用特殊角的三角函数值计算,第四项利用负指数幂法则计算,最后一项分母有理化,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,将m的值代入计算即可求出值.
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,将m的值代入计算即可求出值.
解答:解:(1)原式=-1+1-
+
+
+1=
+1;
(2)原式=
÷
=
•
=-
,
当m=
-3时,原式=-
.
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
(2)原式=
| m-3 |
| 2(m-2) |
| 5-(m+2)(m-2) |
| m-2 |
| m-3 |
| 2(m-2) |
| m-2 |
| -(m+3)(m-3) |
| 1 |
| 2(m+3) |
当m=
| 2 |
| ||
| 4 |
点评:此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
关于x的一元二次方程(k+1)x2-
kx+k-2=0(其中k≠-1,且为常数)的根的情况,描述正确的是( )
| 5 |
| A、无实数根 |
| B、有两个相等的实数根 |
| C、有两个不等的实数根 |
| D、可能只有一个实数根 |
 如图,矩形ABCD中,对角线AC、BD相交于点0,在BC上取BE=BO,连结AE,OE.若∠BOE=75°,则∠CAE的度数等于( )
如图,矩形ABCD中,对角线AC、BD相交于点0,在BC上取BE=BO,连结AE,OE.若∠BOE=75°,则∠CAE的度数等于( )| A、30° | B、45° |
| C、20° | D、15 |
如图是甲、乙两地某年财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )

| A、甲地教育经费占财政经费支出比率较高 |
| B、甲地教育经费支出比较多 |
| C、甲地教育经费支出增幅比较大 |
| D、甲地财政经费支出总额比较小 |
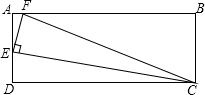 矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
矩形ABCD中,AB=3AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.