题目内容
7.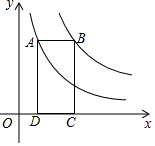 如图,矩形ABCD的顶点C,D在x轴的正半轴上,顶点A,B分别在反比例函数y=$\frac{4}{x}$和y=$\frac{16}{x}$的图象上,则矩形ABCD的面积为12.
如图,矩形ABCD的顶点C,D在x轴的正半轴上,顶点A,B分别在反比例函数y=$\frac{4}{x}$和y=$\frac{16}{x}$的图象上,则矩形ABCD的面积为12.
分析 延长BA交y轴于点E,根据矩形的性质结合反比例函数系数k的几何意义即可得出S矩形ADOE=4、S矩形BCOE=16,二者做差后即可得出矩形ABCD的面积.
解答 解:延长BA交y轴于点E,如图所示.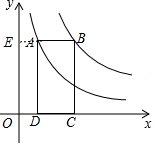
∵四边形ABCD为矩形,点C、D在x轴的正半轴上,
∴BA∥CD,
∴BE⊥y轴.
∵点A、B分别在反比例函数y=$\frac{4}{x}$和y=$\frac{16}{x}$的图象上,
∴S矩形ADOE=4,S矩形BCOE=16,
∴S矩形ABCD=S矩形BCOE-S矩形ADOE=12.
故答案为:12.
点评 本题考查了矩形的性质以及反比例函数系数k的几何意义,根据反比例函数系数k的几何意义找出S矩形ADOE=4、S矩形BCOE=16是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知点D与点A(0,8),B(0,-2),C(x,y)是平行四边形的四个顶点,其中x,y满足x-y+6=0,则CD长的最小值为( )
| A. | $\frac{16}{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 10 |
2.下列四个数中,绝对值比它本身大的数是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 3 |
 如图,直线AB∥CD∥EF,若AC=4,CE=3,则$\frac{BD}{BF}$的值是$\frac{4}{7}$.
如图,直线AB∥CD∥EF,若AC=4,CE=3,则$\frac{BD}{BF}$的值是$\frac{4}{7}$.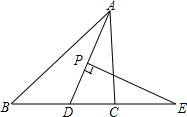 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,若∠B=35°,∠ACB=85°.