题目内容
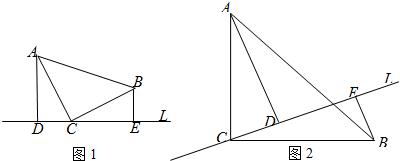
 如图,已知等腰直角△ACB的边AC=BC=a,等腰直角△BED的边BE=DE=b,且a<b,点C、B、E在一条直线上,连接AD.
如图,已知等腰直角△ACB的边AC=BC=a,等腰直角△BED的边BE=DE=b,且a<b,点C、B、E在一条直线上,连接AD.(1)求△ABD的面积;
(2)如果点P是线段CE的中点,连接AP、DP得到△APD,求△APD的面积.
(以上结果先用含a、b代数式表示,后化简)
分析:(1)三角形ABD的面积由梯形ACED的面积-三角形ABC的面积-三角形BDE的面积,表示出关系式,利用完全平方公式化简,去括号合并即可得到结果;
(2)由P为CE的中点,得到CP=PE,由三角形APD的面积=梯形ACED的面积-三角形APC的面积-三角形BEP的面积,利用完全平方公式化简,去括号合并即可得到结果.
(2)由P为CE的中点,得到CP=PE,由三角形APD的面积=梯形ACED的面积-三角形APC的面积-三角形BEP的面积,利用完全平方公式化简,去括号合并即可得到结果.
解答:解:(1)∵AC=BC=a,BE=DE=b,
∴S△ABD=S梯形ACED-S△ABC-S△BDE
=
(a+b)(a+b)-
a2-
b2
=
(a2+2ab+b2-a2-b2)
=ab;
(2)∵P为CE的中点,
∴CP=EP=
(a+b),
∴S△APD=S梯形ACED-S△APC-S△BEP
=
(a+b)(a+b)-
a•
-
b•
=
a2+ab+
b2-
a2-
ab-
ab-
b2
=
(a+b)2.
∴S△ABD=S梯形ACED-S△ABC-S△BDE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=ab;
(2)∵P为CE的中点,
∴CP=EP=
| 1 |
| 2 |
∴S△APD=S梯形ACED-S△APC-S△BEP
=
| 1 |
| 2 |
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| a+b |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
点评:此题考查了整式加减运算的应用,弄清题意列出相应的关系式是解本题的关键.

练习册系列答案
相关题目
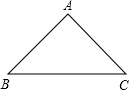 为等腰三角形的生成三角形,简称生成三角形.
为等腰三角形的生成三角形,简称生成三角形.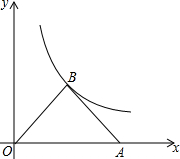 如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线
如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合. 如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.