题目内容
14. 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.则第2016个正方形的边长为($\sqrt{2}$)2015.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.则第2016个正方形的边长为($\sqrt{2}$)2015.
分析 首先求出AC、AE、HE的长度,然后猜测命题中隐含的数学规律,即可解决问题.
解答 解:∵四边形ABCD为正方形,
∴AB=BC=1,∠B=90°,
∴AC2=12+12,AC=$\sqrt{2}$;
同理可求:AE=($\sqrt{2}$)2,HE=($\sqrt{2}$)3…,
∴第n个正方形的边长an=($\sqrt{2}$)n-1,
∴第2016个正方形的边长为($\sqrt{2}$)2015,
故答案为:($\sqrt{2}$)2015.
点评 本题考查了勾股定理在直角三角形中的运用,考查了学生找规律的能力,本题中找到an的规律是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
4.已知某等腰三角形的三边长都是方程x2-3x+2=0的解,则此三角形的周长是( )
| A. | 3或5 | B. | 5或6 | C. | 3或6 | D. | 3或5或6 |
9.下列调查中,适合作全面调查的是( )
| A. | 了解海尔牌电冰箱的市场占有率 | B. | 了解奇瑞牌汽车每百里的耗油量 | ||
| C. | 了解某班级参加课外小组的人数 | D. | 了解某种药品的疗效 |
6.若x>y,则下列式子中错误的是( )
| A. | x+$\frac{1}{3}$>y+$\frac{1}{3}$ | B. | x-3>y-3 | C. | $\frac{x}{3}$>$\frac{y}{3}$ | D. | -3x>-3y |
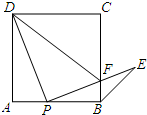 如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.
如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.