题目内容
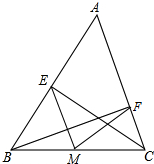 如图所示:CE,BF是△ABC的两条高,M是BC的中点,连ME,MF,∠BAC=50°,则∠EMF的大小是( )
如图所示:CE,BF是△ABC的两条高,M是BC的中点,连ME,MF,∠BAC=50°,则∠EMF的大小是( )| A、50° | B、60° |
| C、70° | D、80° |
考点:直角三角形斜边上的中线
专题:
分析:先由直角三角形斜边上的中线等于斜边的一半得出EM=BM=
BC,那么∠MEB=∠EBM,根据三角形内角和定理得出∠EMB=180°-∠MEB-∠EBM=180°-2∠EBM,
同理∠FMC=180°-2∠FCM,在△ABC中,由三角形内角和定理得出∠ABC+∠ACB=180°-∠BAC=130°,所以∠EMB+∠FMC=180°-2∠EBM+180°-2∠FCM=360°-2(∠EBM+∠FCM)=100°,然后根据平角的定义求出∠EMF=180°-(∠EMB+∠FMC)=80°.
| 1 |
| 2 |
同理∠FMC=180°-2∠FCM,在△ABC中,由三角形内角和定理得出∠ABC+∠ACB=180°-∠BAC=130°,所以∠EMB+∠FMC=180°-2∠EBM+180°-2∠FCM=360°-2(∠EBM+∠FCM)=100°,然后根据平角的定义求出∠EMF=180°-(∠EMB+∠FMC)=80°.
解答:解:∵CE是△ABC的两条高,
∴∠BEC=90°,
∵M是BC的中点,
∴EM=BM=
BC,
∴∠MEB=∠EBM,
∴∠EMB=180°-∠MEB-∠EBM=180°-2∠EBM,
同理∠FMC=180°-2∠FCM,
∵∠BAC=50°,
∴∠ABC+∠ACB=180°-∠BAC=130°,
∴∠EMB+∠FMC=180°-2∠EBM+180°-2∠FCM=360°-2(∠EBM+∠FCM)=100°,
∴∠EMF=180°-(∠EMB+∠FMC)=80°.
故选D.
∴∠BEC=90°,
∵M是BC的中点,
∴EM=BM=
| 1 |
| 2 |
∴∠MEB=∠EBM,
∴∠EMB=180°-∠MEB-∠EBM=180°-2∠EBM,
同理∠FMC=180°-2∠FCM,
∵∠BAC=50°,
∴∠ABC+∠ACB=180°-∠BAC=130°,
∴∠EMB+∠FMC=180°-2∠EBM+180°-2∠FCM=360°-2(∠EBM+∠FCM)=100°,
∴∠EMF=180°-(∠EMB+∠FMC)=80°.
故选D.
点评:本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.同时考查了三角形内角和定理及平角的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于方程组
,把(2)代入(1)得( )
|
| A、2x-6x-1=5 |
| B、2(2x-1)-3y=5 |
| C、2x-6x+3=5 |
| D、2x-6x-3=5 |

 如图,已知AB=AC,DB=DC.这个图形是否轴对称图形?为什么?如果是轴对称图形,它的对称轴是什么?
如图,已知AB=AC,DB=DC.这个图形是否轴对称图形?为什么?如果是轴对称图形,它的对称轴是什么? 如图,D是等边△ABC外的一点,DB=DC,∠BDC=120°,且E、F分别在AB和AC上.
如图,D是等边△ABC外的一点,DB=DC,∠BDC=120°,且E、F分别在AB和AC上.