题目内容
已知(x3+mx+n)(x2-3x+4)的展开式中不含x3和x2项.
(1)求m,n的值;
(2)当m,n取第(1)小题的值时,求(m+n)(m2-mn+n2)的值.
(1)m=-4,n=-12;(2)-1 792. 【解析】试题分析:(1)利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项得出关于m与n的方程组,求出方程组的解即可得到m与n的值; (2)先利用多项式乘以多项式的法则将(m+n)(m2-mn+n2)展开,再合并同类项化为最简形式,然后将(1)中所求m、n的值代入计算即可. 试题解析:【解析】 (1)(x3+mx...
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


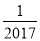 C. -2017 D.
C. -2017 D. 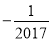
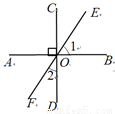
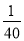 .
.