��Ŀ����
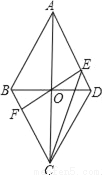
��֪�ı���ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬�Խ���AC��BD���ڵ�O������O��ֱ��EF��AD�ڵ�E����BC�ڵ�F��
��1����֤����AOE�ա�COF��
��2������EOD=30�㣬��CE�ij���
��ϰ��ϵ�д�
 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
�����Ŀ
��Ŀ����
��֪�ı���ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬�Խ���AC��BD���ڵ�O������O��ֱ��EF��AD�ڵ�E����BC�ڵ�F��
��1����֤����AOE�ա�COF��
��2������EOD=30�㣬��CE�ij���

 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�