题目内容
11．
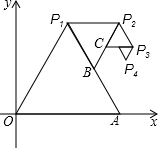如图，以O（0，0）、A（2，0）为顶点作正△OAP1，以点P1和线段P1A的中点B为顶点作正△P1BP2，再以点P2和线段P2B的中点C为顶点作△P2CP3，…，如此继续下去，则第五个正三角形中，不在第四个正三角形上的顶点P5的坐标是（2，$\frac{5\sqrt{3}}{8}$）．
分析 根据三角形的变化找出各三角形的边长，再根据点P的分布，分布找出各P点的坐标即可得出结论．
解答 解：第一个正三角形的边长2，第二个为1，第三个为$\frac{1}{2}$，第四个为$\frac{1}{4}$，第五个为$\frac{1}{8}$，
即OA=2，P1P2=1，P2P3=$\frac{1}{2}$，P3P4=$\frac{1}{4}$，P4P5=$\frac{1}{8}$．
P1（$\frac{1}{2}$OA，$\frac{\sqrt{3}}{2}$OA）=（1，$\sqrt{3}$），P2（1+P1P2，$\sqrt{3}$）=（2，$\sqrt{3}$），P3（2+$\frac{1}{2}$P2P3，$\sqrt{3}$-$\frac{\sqrt{3}}{2}$P2P3）=（$\frac{9}{4}$，$\frac{3\sqrt{3}}{4}$），P4（$\frac{9}{4}$-$\frac{1}{2}$P3P4，$\frac{3\sqrt{3}}{4}$-$\frac{\sqrt{3}}{2}$P3P4）=（$\frac{17}{8}$，$\frac{5\sqrt{3}}{8}$），P5=（$\frac{17}{8}$-P4P5，$\frac{5\sqrt{3}}{8}$）=（2，$\frac{5\sqrt{3}}{8}$）．
故答案为：（2，$\frac{5\sqrt{3}}{8}$）．
点评 本题考查了规律型中的点的坐标，解题的关键是找出各等边三角形的边长．本题属于中档题，难度不大，解决该题型题目时，根据点的坐标的变化找出规律是关键．
练习册系列答案
相关题目
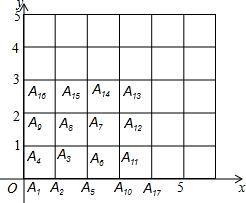如图所示，已知点A1的坐标为（0，0），点A2的坐标为（1，0），点A3的坐标为（1，1），点A4的坐标为（0，1），A5的坐标为（2，0），点A6坐标为（2，1），点A7的坐标为（2，2），点A8的坐标为（1，2），点A9的坐标为（0，2），点A10的坐标为（3，0），点A11的坐标为（3，1），…，依此规律排列下去，则点A25的坐标为（0，4），点A2015的坐标为（34，44）．
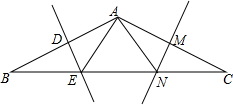在△ABC中，AB=AC，BC=12，∠B=30°，AB的垂直平分线DE交BC边于点E，AC的垂直平分线MN交BC于点N．