Question

2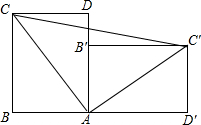．一个直立的火柴盒在桌面上倒下，启发人们发现了勾股定理的一种新的证法．如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a．BC=b，AC=c，请利用四边形BCC′C的面积证明勾股定理．

Answer 1

分析 根据梯形面积公式表示梯形BCC′D′的面积；

解答 解：梯形BCC′D′的面积=$\frac{1}{2}$（a+b）（a+b）=$\frac{1}{2}$（a²+b²）+ab．
S_Rt△CC'A=$\frac{1}{2}$c²，S_Rt△ABC=S_Rt△AD′C=$\frac{1}{2}$ab；
（3）由图形可知S_{梯形BCC′D′}=S_Rt△CC'A+2S_Rt△ABC，
则$\frac{1}{2}$（a+b）（a+b）=$\frac{1}{2}$c²+2×$\frac{1}{2}$ab
∴$\frac{1}{2}$（a²+b²）+ab=$\frac{1}{2}$c²+ab．
因此，a²+b²=c²．

点评 本题考查了勾股定理的证明，需注意：组成的图形的面积有两种表示方法：大的面积的表示方法和各个组成部分的面积的和．