题目内容
11.先化简,再求值.(1)$\frac{{{a^2}+2a+1}}{{{a^2}-1}}-\frac{a}{a-1}$,其中a=3.
(2)$({\frac{3x}{x-1}-\frac{x}{x+1}})$•$\frac{{{x^2}-1}}{x}$,其中$x=\frac{1}{2}$.
分析 (1)先通分,再把分子相加减,分式化为最简分式后把a=3代入进行计算即可;
(2)先算括号里面的,再算乘法,最后把x的值代入进行计算即可.
解答 解:(1)原式=$\frac{(a+1)^{2}}{(a+1)(a-1)}$-$\frac{a}{a-1}$
=$\frac{a+1}{a-1}$-$\frac{a}{a-1}$
=$\frac{1}{a-1}$,
当a=3时,原式=$\frac{1}{2}$;
(2)原式=$\frac{3x(x+1)-x(x-1)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{3{x}^{2}+3x-{x}^{2}+x}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2{x}^{2}+4x}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2x(x+2)}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=2x+4,
当x=$\frac{1}{2}$时,原式=1+4=5.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
1.半径为16cm的圆的内接正三角形的边长为( )
| A. | 16$\sqrt{3}$cm | B. | 8$\sqrt{3}$cm | C. | 4$\sqrt{3}$cm | D. | 16cm |
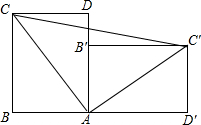 一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理.
一个直立的火柴盒在桌面上倒下,启发人们发现了勾股定理的一种新的证法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a.BC=b,AC=c,请利用四边形BCC′C的面积证明勾股定理. 已知有理数a,b,c在数轴上的位置如图所示,请在数轴上标出-a,-b,-c的位置,并用“<”将a,-a,b,-b,c,-c连接起来.
已知有理数a,b,c在数轴上的位置如图所示,请在数轴上标出-a,-b,-c的位置,并用“<”将a,-a,b,-b,c,-c连接起来.
 已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积.
已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积. 平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.
平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.