Question

18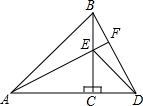．如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，连接BD和AE，延长AE交BD于点F，求证：
（1）△ACE≌△BCD；
（2）AF⊥BD．

Answer 1

分析 先根据SAS判定△ACE≌△BCD即可，从而得到∠EAC=∠DBC，根据角之间的关系以及三角形内角和定理可证得AF⊥BD．

解答 证明：（1）∵△ACB和△ECD都是等腰直角三角形，
∴AC=BC，CE=CD，∠ACE=∠BCD=90°，
在△ACE和△BCD，
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$，
∴△ACE≌△BCD（SAS）；

（2）∵△ACE≌△BCD，
∴∠EAC=∠DBC，
又∵∠DBC+∠CDB=90°，
∴∠EAC+∠CDB=90°，
∴∠AFD=90°，
∴AF⊥BD．

点评 此题主要考查学生对全等三角形的判定及直角三角形的判定的掌握情况．解题时注意：两边及其夹角对应相等的两个三角形全等．