题目内容
1.已知:在△ABC中,CD⊥AB于点D,过点D作DE∥AC,点G为ED的中点,BG的延长线交AC于点F,连接CG.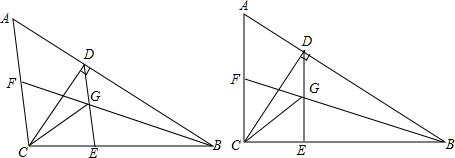
(1)若∠BGE=∠CGE,求证:∠CEG=2∠CDE;
(2)若DE⊥BC,若∠GCE=∠DCG+∠ABF,探究:CE与BE的数量关系.
分析 (1)易证∠CGE=∠DGF和CG=FG,即可证明△CGE≌△FGD,可得∠CEG=∠FDG,易证∠CDF=∠CDE,即可求得∠CDE=$\frac{1}{2}$∠CEG,即可解题;
(2)结论:BE=2CE.如图2中,作CN⊥BF于N,连接FD,取BG中点M,连接EM.首先证明AF=CF=DF=FG,再证明△DGF≌△EGM,推出BG=2CF,由△CGN≌△CGE,推出CE=CN,由△CNF∽△BEG,得到$\frac{CN}{EB}$=$\frac{CF}{BG}$=$\frac{1}{2}$,由此即可证明.
解答 证明:(1)如图1中,连接DF.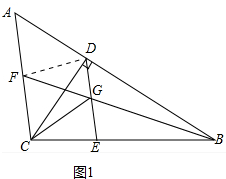
∵DE∥AC,
∴∠CGE=∠ACG,∠BGE=∠BFC,
∵∠CGE=∠BGE,∠BGE=∠DGF,
∴∠ACG=∠BFC,∠CGE=∠DGF,
∴CG=FG,
在△CGE和△FGD中,
$\left\{\begin{array}{l}{CG=FG}\\{∠CGE=∠DGF}\\{DG=GE}\end{array}\right.$,
∴△CGE≌△FGD(SAS),
∴∠CEG=∠FDG,
∵DE∥AC,
∴$\frac{DG}{AF}$=$\frac{BG}{BF}$=$\frac{EG}{FC}$,
∵DG=EG,
∴AF=FC,
∴DF是RT△ACD斜边上中线,
∴∠CDF=∠FCD,
∵∠CDE=∠DCF,
∴∠CDF=∠CDE,
∴∠CDE=$\frac{1}{2}$∠FDG=$\frac{1}{2}$∠CEG
∴2∠CDE=∠CEG;
(2)结论:BE=2CE.
理由:如图2中,作CN⊥BF于N,连接FD,取BG中点M,连接EM.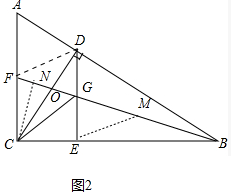
∵∠CNO=∠BDO=90°,∠CON=∠BOD,
∴∠NCO=∠DBO,
∵∠GCE=∠DCG+∠DBG,
∴∠GCE=∠GCN,
∵∠CEG=∠CNG=90°,
∴∠CGE=∠CGN,
∵AC∥DE,
∴∠FCG=∠CGE=∠CGF,
∴FC=FG,
由(1)可知AF=FC,
∴DF=AF=FC=FG,
∴∠FDG=∠FGD=∠EGM,
∵∠BEG=90°,GM=MB,
∴EM=MG=BM,
∴∠MEG=∠MGE=∠FDG,
∵DG=GE,
∴△GDF≌△GEM,
∴FG=GM=BM=FC,
∴BG=2CF,
∵GE∥CF,
∴∠BGE=∠CFN,∵∠CNF=∠BEG=90°,
∴△CNF∽△BEG,
∴$\frac{CN}{EB}$=$\frac{CF}{BG}$=$\frac{1}{2}$,
∴BE=2CN,
在△CGE和△CGN中,
$\left\{\begin{array}{l}{∠CNG=∠CEG}\\{∠CNG=∠CEG}\\{CG=CG}\end{array}\right.$,
∴△CGN≌△CGE,
∴CE=CN,
∴BE=2CE.
点评 本题考查三角形综合题、全等三角形的判定和性质、直角三角形斜边中线定理、相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是添加常用辅助线,构造全等三角形,相似三角形解决问题,综合性比较强,属于中考压轴题.

| A. | |-6| | B. | (-6)-1 | C. | -(-6) | D. | (-6)0 |
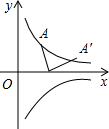 反比例函数y=$\frac{2}{x}$(x>0)和y=-$\frac{2}{x}$(x>0)的图象如图所示,点A的坐标是(1,2),点B(n,0)是x轴上一个动点,连结AB,将线段BA绕点B顺时针旋转90°得到线段BA′.
反比例函数y=$\frac{2}{x}$(x>0)和y=-$\frac{2}{x}$(x>0)的图象如图所示,点A的坐标是(1,2),点B(n,0)是x轴上一个动点,连结AB,将线段BA绕点B顺时针旋转90°得到线段BA′.