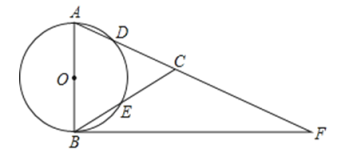
题目内容
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若⊙![]() 的直径为3,
的直径为3,![]() ,求
,求![]() 和
和![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接![]() ,由直径所对的圆周角是直角可得
,由直径所对的圆周角是直角可得![]() ,进而得
,进而得![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,结合已知可得
,结合已知可得![]() ,继而可得
,继而可得![]() ,再根据切线的判定定理即可得;
,再根据切线的判定定理即可得;
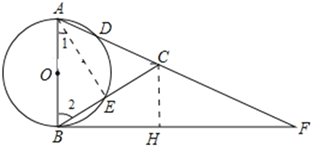
(2)过点C作CH⊥BF于H,由![]() ,
,![]() ,可得
,可得![]() ,可求得
,可求得![]() ,继而可得
,继而可得![]() ,从而求得CH=2,证明△FCH∽△FAB,根据相似三角形的对应边成比例可得
,从而求得CH=2,证明△FCH∽△FAB,根据相似三角形的对应边成比例可得![]() ,可求出CF的长,进行得AF长,再利用勾股定理求出BF的长即可.
,可求出CF的长,进行得AF长,再利用勾股定理求出BF的长即可.
(1)连接![]() ,
,
∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴直线![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)过点C作CH⊥BF于H,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴△FCH∽△FAB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目