题目内容
17.正六边形内接于半径为8的圆,则这个正六边形的面积为96$\sqrt{3}$cm2.分析 设O是正六边形的中心,AB是正六边形的一边,OC是边心距,则△OAB是正三角形,△OAB的面积的六倍就是正六边形的面积.
解答 解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距,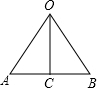
∠AOB=60°,OA=OB=8cm,
则△OAB是正三角形,
∵OC=OA•sin∠A=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$(cm),
∴S△OAB=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×8×4$\sqrt{3}$=16$\sqrt{3}$(cm2),
∴正六边形的面积为16$\sqrt{3}$×6=96$\sqrt{3}$(cm2).
故答案为:96$\sqrt{3}$cm2.
点评 本题考查的正多边形和圆,理解正六边形被半径分成六个全等的等边三角形是解答此题的关键.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | 0、b、3(a-b)都是单项式 | B. | 单项式a没有次数 | ||
| C. | $\frac{1}{x}$是代数式 | D. | x2-2xy-y是由x2、2xy、y2三项组成 |
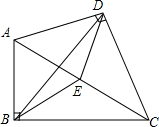 如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点. 画出下列△ABC关于直线l的轴对称图形.
画出下列△ABC关于直线l的轴对称图形.