题目内容
(1)(x+2y)2-(x-2y)(x+2y)
(2)(a-2b+c)(a+2b-c)
(3)(x4y3z-2x3y3+
x2y2)÷
x2y2
(4)(m-n)(m+n)(m2-n2)
(2)(a-2b+c)(a+2b-c)
(3)(x4y3z-2x3y3+
| 1 |
| 4 |
| 1 |
| 2 |
(4)(m-n)(m+n)(m2-n2)
考点:整式的混合运算
专题:
分析:(1)利用完全平方公式和平方差公式计算;
(2)先利用平方差公式计算,再利用完全平方公式计算;
(3)利用多项式除以单项式的方法计算;
(4)先利用平方差公式,再利用完全平方公式计算.
(2)先利用平方差公式计算,再利用完全平方公式计算;
(3)利用多项式除以单项式的方法计算;
(4)先利用平方差公式,再利用完全平方公式计算.
解答:解:(1)原式=x2+4xy+4y2-x2+4y2
=4xy+8y2;
(2)原式=[a-(2b-c)][a+(2b-c)]
=a2-(2b-c)2]
=a2-4b2+4bc-c2;
(3)原式=2x2yz-4xy+
;
(4)原式=(m2-n2)(m2-n2)
=m4-2m2n2+n4.
=4xy+8y2;
(2)原式=[a-(2b-c)][a+(2b-c)]
=a2-(2b-c)2]
=a2-4b2+4bc-c2;
(3)原式=2x2yz-4xy+
| 1 |
| 2 |
(4)原式=(m2-n2)(m2-n2)
=m4-2m2n2+n4.
点评:此题考查整式的混合运算,利用完全平方公式和平方差公式灵活计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
代数式2x-1与3-x的值的符号相同,则x的取值范围是( )
| A、x>3 | ||
B、x<
| ||
C、
| ||
D、x<
|
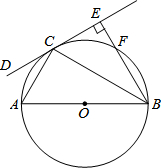 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,交圆与点F,连接AC、BC.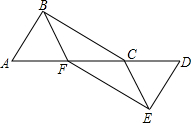 如图,AC=DF,AB=DE,BF=EC.
如图,AC=DF,AB=DE,BF=EC.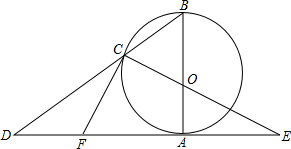 如图,⊙O的直径AB=6cm,DE与⊙O相切于点A,点C为⊙O上的一点,BC的延长线交DE于点D,CO的延长线交DE于点E,过点C作⊙O的切线CF交DE于F,且∠CED的正弦值是方程25x2-15
如图,⊙O的直径AB=6cm,DE与⊙O相切于点A,点C为⊙O上的一点,BC的延长线交DE于点D,CO的延长线交DE于点E,过点C作⊙O的切线CF交DE于F,且∠CED的正弦值是方程25x2-15