题目内容
3. 如图,在?ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=$\sqrt{73}$cm.
如图,在?ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=$\sqrt{73}$cm.
分析 由平行四边形的性质得出BC=AD=8cm,OA=OC=$\frac{1}{2}$AC,由勾股定理求出AC,得出OC,再由勾股定理求出OB即可.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=8cm,OA=OC=$\frac{1}{2}$AC,
∵AC⊥BC,
∴∠ACB=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴OC=3,
∴OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$;
故答案为:$\sqrt{73}$.
点评 本题考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
14.下列事件中,是必然事件的为( )
| A. | 3天内会下雨 | |
| B. | 打开电视机,正在播放广告 | |
| C. | 367人中至少有2人公历生日相同 | |
| D. | 某妇产医院里,下一个出生的婴儿是女孩 |
11. 某几何体的三视图如图所示,则这个几何体是( )
某几何体的三视图如图所示,则这个几何体是( )
 某几何体的三视图如图所示,则这个几何体是( )
某几何体的三视图如图所示,则这个几何体是( )| A. | 球 | B. | 圆柱 | C. | 圆锥 | D. | 三棱柱 |
15.不等式组$\left\{\begin{array}{l}{x+1<3}\\{2x-1>x}\end{array}\right.$的解集是( )
| A. | x>1 | B. | x<2 | C. | 1≤x≤2 | D. | 1<x<2 |
12.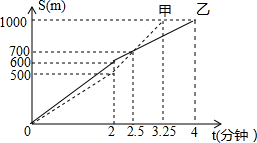 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )| A. | 甲、乙两人进行1000米赛跑 | |
| B. | 甲先慢后快,乙先快后慢 | |
| C. | 比赛到2分钟时,甲、乙两人跑过的路程相等 | |
| D. | 甲先到达终点 |
 如图,正方形ABCD的对角线相交于点O,△OEF是正三角形,且AE=BF,则∠AOE=15°.
如图,正方形ABCD的对角线相交于点O,△OEF是正三角形,且AE=BF,则∠AOE=15°. 如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.