Question

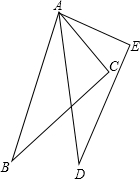如图，∠BAD=∠CAE，AB=AD，AC=AE，则：
（1）△ABC≌△ADE，（2）∠B=∠D，请说明理由．
解：∵∠BAD=

 

（已知）
∴∠BAD+∠DAC=

 

+

 

即

 

在△ABCD与△ADC，中

∴

 

（

 

）
∴∠B=∠D（

 

）

Answer 1

分析：（1）要证△ABC≌△ADE，由已知条件∠BAD=∠CAE，AB=AD，AC=AE，∴∠BAD+∠DAC=∠CAE+∠DAC，所以可以由SAS判定两三角形全等；
（2）因为∠B和∠D为△ABC≌△ADE的对应角，所以相等．

解答：解：∵∠BAD=∠CAE（已知）
∴∠BAD+∠DAC=∠CAE+∠DAC
即∠BAC=∠DAE
在△ABC与△ADE中

AB=AE(已知) ∠BAC=∠DAC AC=AE(已知)

∴△ABC≌△ADE（SAS）
∴∠B=∠D（全等三角形的对应角相等）．

点评：本题考查的三角形全等的判定及应用，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件，全等三角形的对应角相等．