题目内容
如图（1），在Rt△ABC中，∠ACB=90°，D是斜边AB的中点，动点P从B点出发，沿B→C→A运动，设S△DPB=y，点P运动的路程为x，若y与x之间的函数图象如图（2）所示，则△ABC的面
积为
- A.4
- B.6
- C.12
- D.14
B
分析：根据函数的图象知BC=4，AC=3，根据直角三角形的面积的求法即可求得其面积．
解答：∵D是斜边AB的中点，
∴根据函数的图象知BC=4，AC=3，
∵∠ACB=90°，
∴S△ABC=
AC•BC=×3×4=6．
故选B．
点评：本题考查了动点问题的函数图象，要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．
分析：根据函数的图象知BC=4，AC=3，根据直角三角形的面积的求法即可求得其面积．
解答：∵D是斜边AB的中点，
∴根据函数的图象知BC=4，AC=3，
∵∠ACB=90°，
∴S△ABC=
AC•BC=×3×4=6．故选B．
点评：本题考查了动点问题的函数图象，要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
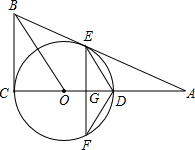（2012•中江县二模）如图，⊙O的圆心在Rt△ABC的直角边AC上，⊙O经过C、D两点，与斜边AB交于点E，连接BO、ED，且BO∥ED，作弦EF⊥AC于G，连接DF．
如图，已知：在Rt△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于D．
如图，已知：在Rt△ABC中，∠C=90°，E为AB的中点，且DE⊥AB于E，若∠CAD：∠DAB=1﹕2，求∠B的度数．