题目内容
4.深化理解:新定义:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$,则<x>=n;
反之,当n为非负整数时,如果<x>=n,则n-$\frac{1}{2}$≤x<n+$\frac{1}{2}$.
例如:<0>=<0.48>=0,<0.64>=<1.49>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>=3(π为圆周率); ②如果<x-1>=3,则实数x的取值范围为3.5≤x<4.5.
(2)若关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-4}{3}≤x-1}\\{<a>-x>0}\end{array}\right.$的整数解恰有3个,求a的取值范围.
(3)求满足<x>=$\frac{4}{3}$x 的所有非负实数x的值.
分析 (1)①利用对非负实数x“四舍五入”到个位的值记为<x>,进而得出<π>的值;
②利用对非负实数x“四舍五入”到个位的值记为<x>,进而得出x的取值范围;
(2)首先将<a>看作一个字母,解不等式组进而根据整数解的个数得出a的取值范围;
(3)利用<x>=$\frac{4}{3}$x 设$\frac{4}{3}$x=k,k为整数,得出关于k的不等关系求出即可.
解答 解:(1)①由题意可得:<π>=3;
故答案为:3,
②∵<x-1>=3,
∴2.5≤x-1<3.5
∴3.5≤x<4.5;
故答案为:3.5≤x<4.5;
(2)解不等式组得:-1≤x<<a>,
由不等式组整数解恰有3个得,1<<a>≤2,
故1.5≤a<2.5;
(3)∵x≥0,$\frac{4}{3}$x为整数,
设$\frac{4}{3}$x=k,k为整数,则x=$\frac{3}{4}$k,
∴<$\frac{3}{4}$k>=k,
∴k-$\frac{1}{2}$≤$\frac{3}{4}$k<k+$\frac{1}{2}$,k≥o,
∴0≤k≤2,
∴k=0,1,2,
则x=0,$\frac{3}{4}$,$\frac{3}{2}$.
点评 此题主要考查了新定义以及一元一次不等式的应用,根据题意正确理解<x>的意义是解题关键.

练习册系列答案
相关题目
9.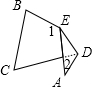 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
 如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
如图:把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )| A. | ∠1=∠2+∠A | B. | ∠1=2∠A+∠2 | C. | ∠1=2∠2+2∠A | D. | 2∠1=∠2+∠A |
13. 如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
 如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )
如图,小半圆的直径与大半圆的直径AB重合,圆心重合,弦CD与小半圆相切,CD=10,则阴影部分面积为( )| A. | 100π | B. | 50π | C. | 25π | D. | 12.5π |
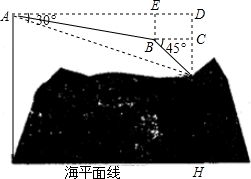 2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:
2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算: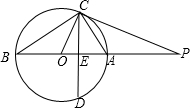 如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.
如图,AB是⊙O的直径,点P在BA的延长线上,点A是$\widehat{CD}$的中点,∠POC=∠PCE.


