��Ŀ����
 ��֪���κ���ͼ��ΪC��1��0����ֱ��y=x+m��ö��κ�������A��B���㣬����A�㣨3��4����B����y���ϣ�
��֪���κ���ͼ��ΪC��1��0����ֱ��y=x+m��ö��κ�������A��B���㣬����A�㣨3��4����B����y���ϣ���1����˶��κ����Ľ���ʽ��
��2��PΪ�߶�AB��һ���㣨����A��B�غϣ�������P��y���ƽ��������κ������ڵ�E�����߶�PE��Ϊh����P������Ϊx����h��x֮��ĺ�����ϵʽ��
��3��DΪ�߶�AB����κ����Գ���Ľ��㣬��AB���Ƿ����һ��P��ʹ�ı���DCEPΪƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1�����Ƚ�A��3��4������y=x+m�ó�m��ֵ�����ɵó�B�����꣬�������ô���ϵ��������κ�������ʽ���ɣ�
��2����ʾ��E��P�����꣬���������߶�PE�ó����ɣ�
��3�����ȵó�D�����꣬��������ƽ���ı��ε����ʵó�P������꣬���ɵó��𰸣�
��2����ʾ��E��P�����꣬���������߶�PE�ó����ɣ�
��3�����ȵó�D�����꣬��������ƽ���ı��ε����ʵó�P������꣬���ɵó��𰸣�
����⣺��1����A��3��4������y=x+m
��m=1��
��y=x+1��
��B��0��1����
����κ�������ʽΪy=ax2+bx+c��
��A��B��C������������
��
���
��
����κ����Ľ���ʽΪ��y=x2-2x+1��
��2����P����ֱ��y=x+1��ͼ����
��P��������x��x+1����
��E����������y=x2-2x+1��ͼ���ϣ�
��E��������x��x2-2x+1����
��h=��x+1��-��x2-2x+1��=-x2+3x��
��3�����ڣ�
�������߶Գ���Ϊֱ��x=-
=1��
�൱x=1ʱ��y=x+1=2��
��D��������1��2����
��DC=2��
��PE=2ʱ��PE��DC���ı���DCEPΪƽ���ı��Σ�
��-x2+3x=2��
��ã�x1=1��x2=2��
��x=1ʱ��PE��DC�غϣ�
��x=2ʱ������y=x+1����ã�y=3��
��P��������2��3����
��m=1��
��y=x+1��
��B��0��1����
����κ�������ʽΪy=ax2+bx+c��
��A��B��C������������
|
���
|
����κ����Ľ���ʽΪ��y=x2-2x+1��
��2����P����ֱ��y=x+1��ͼ����
��P��������x��x+1����
��E����������y=x2-2x+1��ͼ���ϣ�
��E��������x��x2-2x+1����
��h=��x+1��-��x2-2x+1��=-x2+3x��
��3�����ڣ�
�������߶Գ���Ϊֱ��x=-
| b |
| 2a |
�൱x=1ʱ��y=x+1=2��
��D��������1��2����
��DC=2��
��PE=2ʱ��PE��DC���ı���DCEPΪƽ���ı��Σ�
��-x2+3x=2��
��ã�x1=1��x2=2��
��x=1ʱ��PE��DC�غϣ�
��x=2ʱ������y=x+1����ã�y=3��
��P��������2��3����
������������Ҫ�����˶��κ������ۺ��Լ�ƽ���ı��ε����ʺʹ���ϵ��������κ�������ʽ��֪ʶ���������ν�ϵó���ʾ��PE�ij��ǽ���ؼ���

��ϰ��ϵ�д�
 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
�����Ŀ
 ��1���ⷽ�̣�x2+3x+1=0
��1���ⷽ�̣�x2+3x+1=0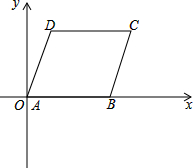 ��ƽ��ֱ������ϵ�У��߳�Ϊ2������ABCD�Ķ���A������ԭ��O�غϣ�AB����x����������ϣ���C=60��
��ƽ��ֱ������ϵ�У��߳�Ϊ2������ABCD�Ķ���A������ԭ��O�غϣ�AB����x����������ϣ���C=60�� ��ͼ����һ��С���б��OA��O�㴦�׳�������б�µ�A�㴦��С����׳�·���������ߵ�һ�Σ����ĶԳ���l�ֱ���OA��x���ཻ�ڵ�B��C������P�ĺ�������4��б��OA���½�Ϊ����
��ͼ����һ��С���б��OA��O�㴦�׳�������б�µ�A�㴦��С����׳�·���������ߵ�һ�Σ����ĶԳ���l�ֱ���OA��x���ཻ�ڵ�B��C������P�ĺ�������4��б��OA���½�Ϊ����