Question

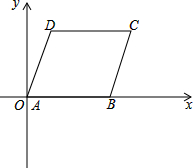在平面直角坐标系中，边长为2的菱形ABCD的顶点A与坐标原点O重合，AB边在x轴的正半轴上，∠C=60°
（1）求C点坐标；
（2）求经过A，B，C三点的抛物线对应的函数关系式．

Answer 1

考点：菱形的性质,待定系数法求二次函数解析式

专题：

分析：（1）首先过点C作CE⊥x轴于点E，由边长为2的菱形ABCD的顶点A与坐标原点O重合，AB边在x轴的正半轴上，∠C=60°，可求得C点坐标；
（2）首先设经过A，B，C三点的抛物线对应的函数关系式为y=ax²+bx+c，然后利用待定系数法即可求得二次函数的解析式．

解答：解：（1）过点C作CE⊥x轴于点E，
∵四边形ABCD是菱形，
∴AB∥CD，
∴∠CBE=∠BCD=60°，
∴∠BCE=30°，
∴BE=

1

2

BC=

1

2

×2=1，
∴CE=

BC2-BE2

=

3

，AE=AB+BE=2+1=3，
∴点C的坐标为：（3，

3

）；

（2）设经过A，B，C三点的抛物线对应的函数关系式为y=ax²+bx+c，
根据题意得：A（0，0），B（2，0），
∴

c=0 4a+2b+c=0 9a+3b+c= 3

，
解得：

a= 3 3 b=- 2 3 3 c=0

，
∴经过A，B，C三点的抛物线对应的函数关系式为y=

3

3

x²-

2 3

3

x．

点评：此题考查了菱形的性质以及待定系数法求二次函数的解析式．此题难度适中，注意掌握辅助线的作法，注意掌握方程思想与数形结合思想的应用．