题目内容
7. 如图,在直角三角形ABC中,∠A=90°,DE是BC边上的垂直平分线,CE恰好是∠ACB的平分线,则:
如图,在直角三角形ABC中,∠A=90°,DE是BC边上的垂直平分线,CE恰好是∠ACB的平分线,则:(1)∠B等于多少?
(2)若DE=4,且DE:CE=1:2,则S△ABC等于多少?
分析 (1)根据已知求出∠ACE=∠BCE,CE=BE,求出∠B=∠ECB=∠ACE,根据三角形内角和定理求出即可;
(2)求出AE、BE,求出AB,解直角三角形求出AC,根据三角形面积公式求出即可.
解答 解:(1)∵在直角三角形ABC中,∠A=90°,DE是BC边上的垂直平分线,CE恰好是∠ACB的平分线,
∴∠ACE=∠BCE,CE=BE,
∴∠B=∠ECB=∠ACE,
∴3∠B=90°,
∴∠B=30°;
(2)∵在直角三角形ABC中,∠A=90°,DE是BC边上的垂直平分线,CE恰好是∠ACB的平分线,
∴AE=DE,∠CDE=90°,CE=BE,
∵DE:CE=1:2,DE=4,
∴CE=BE=2DE=8,AE=4,
∴AB=12,
∵∠B=30°,
∴BC=2AC,
∴AC=$\frac{12}{\sqrt{3}}$=4$\sqrt{3}$,
∴S△ACB=$\frac{1}{2}×AB×AC$=$\frac{1}{2}×12×4\sqrt{3}$=24$\sqrt{3}$.
点评 本题考查了角平分线性质和线段垂直平分线性质的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
19.下列去括号正确的是( )
| A. | a+3(b+8)=a+3b+8 | B. | 2m-3(n-6)=2m-3n-18 | ||
| C. | -(a+b)-1=-a-b-1 | D. | 4xy-3(-x+y)=4xy-3x-3y |
 如图,抛物线y=-x2+bx+c与x轴交于点M,N,与y轴交于点A(0,1),且经过点B(1,1),过点B作BC⊥x轴,交x轴于点C.
如图,抛物线y=-x2+bx+c与x轴交于点M,N,与y轴交于点A(0,1),且经过点B(1,1),过点B作BC⊥x轴,交x轴于点C.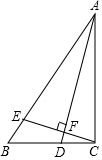 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为边BC上一动点(不与点B、C重合),联结AD,过点C作CF⊥AD,分别交AB、AD于点E、F,设DC=x,$\frac{AE}{BE}$=y.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为边BC上一动点(不与点B、C重合),联结AD,过点C作CF⊥AD,分别交AB、AD于点E、F,设DC=x,$\frac{AE}{BE}$=y. 综合与探究
综合与探究 如图,平面直角坐标系中,已知点A(a-b,2$\sqrt{3}$),B(a+b,0),AB=4,且$\sqrt{a-3b}$+(a+b-4)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
如图,平面直角坐标系中,已知点A(a-b,2$\sqrt{3}$),B(a+b,0),AB=4,且$\sqrt{a-3b}$+(a+b-4)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.