题目内容

4．二次函数y=ax2+bx+c的图象如图，点（1，0）在函数图象上，那么abc、2a+b、a+b+c、a-b+c这四个代数式中，值大于或等于零的数有（　　）
A．1个B．2个C．3个D．4个

分析 由抛物线开口向上，a＞0，由对称轴-$\frac{b}{2a}$＞0，可得b＜0，抛物线与y轴交点为负半轴，可知c＜0，再根据特殊点进行推理判断即可求解．

解答 解：由抛物线开口向上，a＞0，由对称轴-$\frac{b}{2a}$＞0，
∴b＜0，
∵抛物线与y轴交点为负半轴，可知c＜0，
∴abc＞0；
∵对称轴-$\frac{b}{2a}$＜1，
∴2a+b＞0；
当x=1时，y=a+b+c=0；
当x=-1时，y=a-b+c＞0．
故值为正的有3个．
故选：C．

点评 此题考查了二次函数图象与系数的关系，属于基础题，关键是掌握根据图象获取信息的能力．

练习册系列答案
相关题目
8．解方程、计算
（1）3x2-5x=0                
（2）x2+2x-3=5（限用配方法）
（3）（x-2）2-5（x-2）-6=0       
（4）计算2$\sqrt{\frac{1}{8}}$-$\sqrt{\frac{1}{2}}$-（$\sqrt{18}$+$\sqrt{2}$-2$\sqrt{\frac{1}{3}}$）
15．若m，n都是正整数，且1≤n＜m则下列按字母x的降幂排列是（　　）
A．xm+yn-2xyB．yn+xm-2xyC．xm-2xy+ynD．yn-2xy+xm
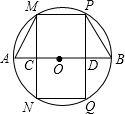12．如图，AB是⊙O直径，C、D是AB上两点，MC⊥AB交⊙O于M、N，PD⊥AB交⊙O于P、Q，
（1）求证：PM=QN；
（2）若AC=BD，求证：$\widehat{AM}$=$\widehat{BP}$；
（3）若AM=MP=PB，求证：C为OA中点．
19．化简：
$\frac{1}{m×（m+n）}$+$\frac{1}{（m+n）（m+2n）}$+$\frac{1}{（m+2n）（m+3n）}$+…+$\frac{1}{（m+99n）（m+100n）}$．
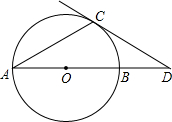9．如图，AB是⊙O的直径，点D在AB的延长线上，BD=OB，点C在圆上，∠CAB=30°．
（1）求证：DC是⊙O的切线． 
（2）若BD=1cm，求AC的长．
16．解方程 
（1）2y=-y+3   
（2）3（2x+5）-2（4x-3）=22   
（3）$\frac{x-3}{2}$=$\frac{4x-1}{5}$-4．
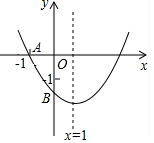13．如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（-1，0），与y轴的交点B在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③4ac-b2＜16a；④$\frac{1}{3}$＜a＜$\frac{2}{3}$；⑤b＞c．
其中正确结论的序号是①③④⑤．
14．四人做传数游戏，小郑任报一个数给小丁，小丁把这个数加1传给小红，小红再把所得的数乘以2后传给小童，小童把所听到的数减1报出答案．
（1）如果小郑所报的数为x，请把小童最后所报的答案用代数式表示出来
（2）若小郑报的数为9，则小童的答案是多少？
（3）若小童报出的答案是15，则小郑传给小丁的数是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网