题目内容
在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
A.22 B.24 C. D.
D.
B.
【解析】
试题分析:如图:

∵直线y=kx-3k+4必过点D(3,4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,4),
∴OD=5,
∵以原点O为圆心的圆过点A(13,0),
∴圆的半径为13,
∴OB=13,
∴BD=12,
∴BC的长的最小值为24.
故选B.
考点:1.垂径定理;2.一次函数图象上点的坐标特征;3.勾股定理.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
根据下表中的二次函数 的自变量x与函数y的对应值,可判断二次函数的图象与x轴( )
的自变量x与函数y的对应值,可判断二次函数的图象与x轴( )
x | …… | -1 | 0 | 1 | 2 | …… |
y | …… | -1 | - | -2 |
| …… |
A、只有一个交点
B、有两个交点,且它们分别在y轴两侧
C、有两个交点,且它们均在y轴同侧
D、无交点

 是方程
是方程 的一个根,求
的一个根,求 的值及方程的另一个根.
的值及方程的另一个根.
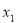 、
、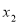 是一元二次方程
是一元二次方程 的两个根,则
的两个根,则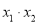 等于( )
等于( )

