题目内容
9.用配方法解方程:(1)x2-2x=4;
(2)2x2+3=-5x.
分析 (1)利用完全平方公式配方,开方即可求出解.
(2)方程变形后,利用完全平方公式配方,开方即可求出解.
解答 解:(1)配方得:x2-2x+1=5,即(x-1)2=5,
开方得:x-1=±$\sqrt{5}$,
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$;
(2)方程整理得:x2+$\frac{5}{2}$x=-$\frac{3}{2}$,
配方得:x2+$\frac{5}{2}$x+$\frac{25}{16}$=-$\frac{3}{2}$+$\frac{25}{16}$,即(x+$\frac{5}{4}$)2=$\frac{1}{16}$,
开方得:x+$\frac{5}{4}$=±$\frac{1}{4}$,
解得:x1=-1,x2=-$\frac{3}{2}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
20.某商店举办促销活动,促销的方法是将原价x元的衣服以($\frac{9}{10}$x-15)元出售,则下列说法中,能正确表达该商店促销方法的是( )
| A. | 原价减去15元后再打9折 | B. | 原价打9折后再减去15元 | ||
| C. | 原价减去15元后再打1折 | D. | 原价打1折后再减去15元 |
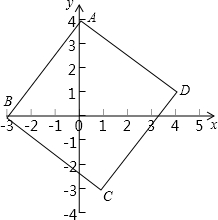 正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求C、D两点的坐标.
正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求C、D两点的坐标.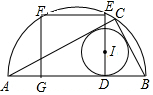 如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为81.
如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为81.