题目内容
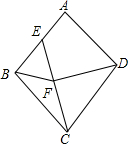 已知,如图,在菱形ABCD中,点E为AB边的中点,连接CE,点F为CE上的一点且2∠BFE+∠A=180°,连接DF,则∠CFD=
已知,如图,在菱形ABCD中,点E为AB边的中点,连接CE,点F为CE上的一点且2∠BFE+∠A=180°,连接DF,则∠CFD=考点:菱形的性质
专题:
分析:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.构建相似三角形△EBG∽△EFB、△GOF∽△GCD,进而推知△DFG∽△COG,则其对应角相等:∠GFD=∠GOC=90°.
解答: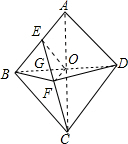 解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.
解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠EBG+∠BAO=90°,
又∵2∠BFE+∠A=180°,
∴∠EFB+∠BAO=90°,
∴∠EBG=∠EFB,
又∠BEG=∠FBE,
∴△EBG∽△EFB,
∴BE2=EG•EF,EB=EO,
∴△EGO∽△EOF,
∴∠EOG=∠EFO=∠ABD=∠GDC,∠FGO=∠OGD,
∴△GOF∽△GCD,
∴
=
,
∴
=
,
∵∠CGO=∠DGF,
∴△DFG∽△COG,
∴∠GFD=∠GOC=90°.
故答案是:90°.
 解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.
解:如图,连接AC、BD,AC与BD交于点O,连接EO、FO.∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠EBG+∠BAO=90°,
又∵2∠BFE+∠A=180°,
∴∠EFB+∠BAO=90°,
∴∠EBG=∠EFB,
又∠BEG=∠FBE,
∴△EBG∽△EFB,
∴BE2=EG•EF,EB=EO,
∴△EGO∽△EOF,
∴∠EOG=∠EFO=∠ABD=∠GDC,∠FGO=∠OGD,
∴△GOF∽△GCD,
∴
| GO |
| GC |
| GF |
| GD |
∴
| GO |
| GF |
| GC |
| GD |
∵∠CGO=∠DGF,
∴△DFG∽△COG,
∴∠GFD=∠GOC=90°.
故答案是:90°.
点评:本题考查了菱形的性质.解题时,注意辅助线的作法,此题是通过作辅助线构建相似三角形,利用相似三角形的性质进行证明的.

练习册系列答案
相关题目
 在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )
在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )| A、x2+65x-350=0 |
| B、x2+130x-1400=0 |
| C、x2-65x-350=0 |
| D、x2-130x-1400=0 |
下面每组中的两个数互为相反数的是( )
A、-
| ||
B、-2.5和2
| ||
| C、8和-(-8) | ||
D、
|
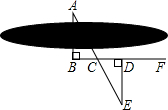 如图,要测量河岸相对两点A,B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一直线上,可以证明△EDC≌△ABC得ED=AB,因此测得DE的长度就是AB的长,判断△EDC≌△ABC的理由是( )
如图,要测量河岸相对两点A,B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在同一直线上,可以证明△EDC≌△ABC得ED=AB,因此测得DE的长度就是AB的长,判断△EDC≌△ABC的理由是( )| A、边边边 | B、边角边 |
| C、角边角 | D、边边角 |
某商场2012年的销售利润为2亿元,预计以后每年比上一年增长10%,那么2014年该商场的销售利润将是( )
| A、2.42亿元 |
| B、2.4亿元 |
| C、2.2亿元 |
| D、4.4亿元 |
 已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.
已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.