题目内容
5.已知菱形ABCD中,对角线AC与BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )| A. | 16$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
分析 由菱形的性质得出AB=BC,OA=$\frac{1}{2}$AC=2,OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD+∠ABC=180°,再证明△ABC是等边三角形,得出AB=AC=4,根据勾股定理求出OB,得出BD,由菱形的面积=$\frac{1}{2}$AC•BD,即可得出结论.
解答 解:∵四边形ABCD是菱形,
∴AB=BC,OA=$\frac{1}{2}$AC=2,OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=4,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴BD=2OB=4$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$;
故选:B.
点评 本题考查了菱形的性质、等边三角形的判定与性质、勾股定理、菱形面积的计算;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
15.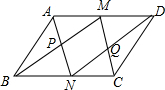 如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
 如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )| A. | AP=PN | B. | NQ=QD | ||
| C. | 四边形PQNM是矩形 | D. | △ABN是等边三角形 |