题目内容
20.我们知道$\sqrt{2}≈1.414$,于是我们说:“$\sqrt{2}$的整数部分为1,小数部分则可记为$\sqrt{2}-1$”.已知3+$\sqrt{32}$的小数部分为a,7-$\sqrt{32}$的小数部分为b,那么a+b的值是多少?分析 首先求出$\sqrt{32}$的取值范围,进而表示出a,b的值,进而得出答案.
解答 解:∵5<$\sqrt{32}$<6,
∴3+$\sqrt{32}$的小数部分为a时,则a=3+$\sqrt{32}$-8=$\sqrt{32}$-5,
∴7-$\sqrt{32}$的小数部分为b时,则b=7-$\sqrt{32}$-1=6-$\sqrt{32}$,
∴a+b=$\sqrt{32}$-5+6-$\sqrt{32}$=1.
点评 此题主要考查了估算无理数的大小,得出a,b的值是解题关键.

练习册系列答案
相关题目
8. 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )| A. | b<a | B. | a+b<0 | C. | ab<0 | D. | b-a>0 |

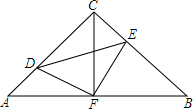 如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.
如图,在△ABC中,∠A=∠B=45°,AC=8,F是AB边上的中点,点D,E分别在AC,BC上,且AD=CE,CF=AF.则四边形CDFE的面积是16.