��Ŀ����
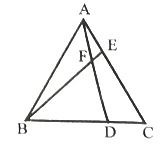
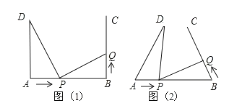
����Ŀ����ͼ��1����![]() ��
��![]() ��
��![]() ����ΪA��B��
����ΪA��B��![]() ����
����![]() ���߶�
���߶�![]() ����ÿ��2
����ÿ��2![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶���ͬʱ��
�˶���ͬʱ��![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ���
���![]() �˶��������˶���ʱ��Ϊ
�˶��������˶���ʱ��Ϊ![]() ��
��![]() ����
����
��1��![]() ��������
�������� ![]() ��
��![]() ��������
�������� ![]() ������
������![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2�����![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶ���ȣ���
���˶��ٶ���ȣ���![]() ʱ��
ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ����жϴ�ʱ�߶�
�Ƿ�ȫ�ȣ����жϴ�ʱ�߶�![]() ���߶�
���߶�![]() ��λ�ù�ϵ����ֱ�˵�����ɣ�
��λ�ù�ϵ����ֱ�˵�����ɣ�
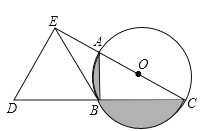
��3����ͼ��2������ͼ��1���еġ�![]() ��
��![]() ��������
������Ϊ��![]() ���������������䣮���
���������������䣮���![]() ���˶��ٶ�Ϊ
���˶��ٶ�Ϊ![]()
![]() ���Ƿ����������
���Ƿ����������![]() ��
��![]() ��
��![]() �Ƿ�ȫ�ȣ������ڣ������Ӧ��x��t��ֵ���������ڣ���˵�����ɣ�
�Ƿ�ȫ�ȣ������ڣ������Ӧ��x��t��ֵ���������ڣ���˵�����ɣ�
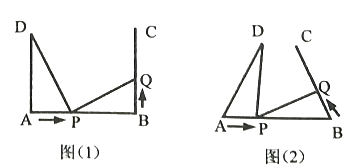
���𰸡���1��2t��8-2t����2����ADP���BPQȫ�ȣ��߶�PD���߶�PQ��ֱ�����ɼ���������3������![]() ��
��![]() ��ʹ�á�ADP���BPQȫ�ȣ�
��ʹ�á�ADP���BPQȫ�ȣ�
��������
��1����������ֱ�ӿɵô�.
��2����t=1�ɵá�ACP�͡�BPQ�и��ߵij�����SAS�Ƴ���ACP�ա�BPQ����������ȫ�����������ʵá�APC+��BPQ=90�㣬�ݴ��ж��߶�PC��PQ��λ�ù�ϵ��
��3�������ACP�ա�BPQ����t��x��ʾ���߳������ݶ�Ӧ����Ƚ��t��x��ֵ��
�ټ����ACP�ա�BQP�����ϲ��ķ�����⣬ע���ʱ�Ķ�Ӧ�ߺ��ϲ���һ��.
��1��������ã�![]() 2t��
2t��![]() 8-2t��
8-2t��
��2����ADP���BPQȫ�ȣ��߶�PD���߶�PQ��ֱ��
�������£�
��t=1ʱ��AP=BQ=2��BP=AD=6��
�֡�A=��B=90�㣬
�ڡ�ADP�͡�BPQ�У�
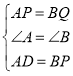 �����ADP
�����ADP![]() ��BPQ��SAS�������ADP=��BPQ�����APD+��BPQ=��APD+��ADP=90�㣬���DPQ=90�㣬���߶�PD���߶�PQ��ֱ��
��BPQ��SAS�������ADP=��BPQ�����APD+��BPQ=��APD+��ADP=90�㣬���DPQ=90�㣬���߶�PD���߶�PQ��ֱ��
��3��������ADP![]() ��BPQ��
��BPQ��
��AD=BP����AP=BQ��
��![]() ��
��
���![]() ��
��
������ADP![]() ��BQP��
��BQP��
��AD=BQ��AP=BP��
��![]() ��
��
��ã�![]() ��
��
��������������![]() ��
��![]() ��ʹ�á�ADP���BPQȫ�ȣ�
��ʹ�á�ADP���BPQȫ�ȣ�

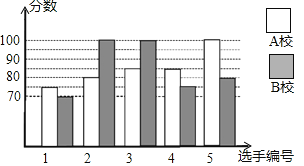
����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
![]() ����ͼʾ��д�±���
����ͼʾ��д�±���
ƽ���� | ��λ�� | ���� | |
AУ | ______ | 85 | ______ |
BУ | 85 | ______ | 100 |
![]() �����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
�����У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
![]() ������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���
������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���