题目内容
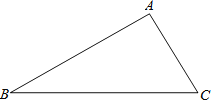
【题目】如图，已知点
，
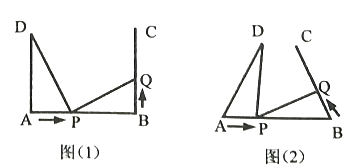
，点C是直线AB上异于点B的任一点，现以BC为一边在AB右侧作正方形BCDE，射线OC与直线DE交于点P，若点C的横坐标为m．
求直线AB的函数表达式．
若点C在第一象限，且点C为OP的中点，求m的值．
若点C为OP的三等分点
即点C分OP成1：2的两条线段
，请直接写出点C的坐标．
【答案】（1）
；（2）
；（3）
或
或
或
【解析】
（1）利用待定系数法即可解决问题；
（2）如图，作OG⊥BC于G，OH⊥OB于H．只要证明△OCG≌△CPD，利用全等三角形的性质可得OG=CD，由此构建方程即可解决问题；
（3）在第一象限和第二象限分两种情形，分别构建方程求出m即可解决问题；
解：
设直线AB的解析式为
，
把
，
代入得到
，
解得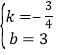
，
直线AB的解析式为．
如图，作
于G，
于H．
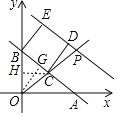
四边形BCDE是正方形，
，
，
，
，
≌
，
，
，
，
，
，
，
，
，
．
当点C中第一象限，
时，
∽，
：
：1，
，
，
，
，
∴C（
，
）
当点C中第一象限，
时，．
∽，
：
：2，
，
，
，
，
∴C（
，
）
当点C中第二象限，时，．
∽，
：：2，
，
，
，
，
∴C（
，
）.
当点C中第二象限，时，
∽，
：：1，
，
，
，
，
∴C（
，
）
综上所述，满足条件的点C坐标为或或或
练习册系列答案
相关题目
